
【题目】(1)如图①,一个无盖的长方体盒子的棱长分别为![]() ,
,![]() ,
,![]() ,盒子的内部顶点
,盒子的内部顶点![]() 处有一只昆虫甲,在盒子的内部顶点
处有一只昆虫甲,在盒子的内部顶点![]() 处有一只昆虫乙(盒壁的厚度忽略不计)假设昆虫甲在顶点
处有一只昆虫乙(盒壁的厚度忽略不计)假设昆虫甲在顶点![]() 处静止不动,请计算
处静止不动,请计算![]() 处的昆虫乙沿盒子内壁爬行到昆虫甲
处的昆虫乙沿盒子内壁爬行到昆虫甲![]() 处的最短路程,并画出其最短路径,简要说明画法
处的最短路程,并画出其最短路径,简要说明画法
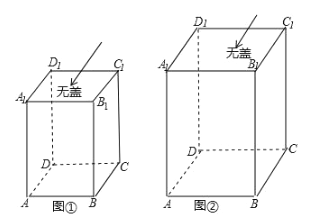
(2)如果(1)问中的长方体的棱长分别为![]() ,
,![]() ,如图②,假设昆虫甲从盒内顶点
,如图②,假设昆虫甲从盒内顶点![]() 以1厘米/秒的速度在盒子的内部沿棱
以1厘米/秒的速度在盒子的内部沿棱![]() 向下爬行,同时昆虫乙从盒内顶点
向下爬行,同时昆虫乙从盒内顶点![]() 以3厘米/秒的速度在盒壁的侧面上爬行,那么昆虫乙至少需要多长时间才能捕捉到昆虫甲?
以3厘米/秒的速度在盒壁的侧面上爬行,那么昆虫乙至少需要多长时间才能捕捉到昆虫甲?
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图甲,点C将线段AB分成两部分(AC>BC),如果![]() =
=![]() ,那么称点C为线段AB的黄金分割点.某数学兴趣小组在进行课题研究时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成面积分别为S1,S2(S1>S2)的两部分,如果
,那么称点C为线段AB的黄金分割点.某数学兴趣小组在进行课题研究时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成面积分别为S1,S2(S1>S2)的两部分,如果![]() =
=![]() ,那么称直线l为该图形的黄金分割线.
,那么称直线l为该图形的黄金分割线.
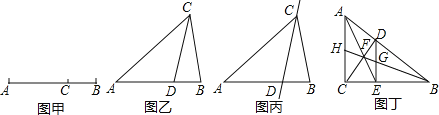
(1)如图乙,在△ABC中,∠A=36°,AB=AC,∠ACB的平分线交AB于点D,请问点D是否是AB边上的黄金分割点,并证明你的结论;
(2)若△ABC在(1)的条件下,如图丙,请问直线CD是不是△ABC的黄金分割线,并证明你的结论;
(3)如图丁,在Rt△ABC中,∠ACB=90°,D为斜边AB上的一点,(不与A,B重合)过D作DE⊥BC于点E,连接AE,CD相交于点F,连接BF并延长,与DE,AC分别交于点G,H.请问直线BH是直角三角形ABC的黄金分割线吗?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A(-4,![]() ),B(-1,2)是一次函数y=kx+b的图像与反比例函数
),B(-1,2)是一次函数y=kx+b的图像与反比例函数![]() (m≠0,m<0)的函数图像的两个交点,AC⊥x轴于点C,BD⊥y轴于点D
(m≠0,m<0)的函数图像的两个交点,AC⊥x轴于点C,BD⊥y轴于点D
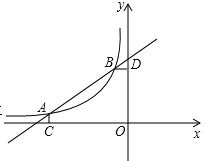
(1)根据函数图像直接回答问题:在第二象限内,当x取何值时,一次函数的值大于反比例函数的值?
(2)求一次函数的表达式及m的值;
(3)点P是线段AB上一点,连接PC,PD,若△PCA和△PBD的面积相等,求点P的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店把一商品按标价的九折出售(即优惠10%),仍可获利20%,若该商品的标价为每件28元,则该商品的进价为( )
A.21元
B.19.8元
C.22.4元
D.25.2元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() (k为常数,k≠0)的图像经过点A(2,3)。
(k为常数,k≠0)的图像经过点A(2,3)。
(1)求这个函数的解析式;
(2)判断点B(-1,6),C(3,2)是否在这个函数图像上;
(3)当-3<x<-1时,求y的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某乡镇要在生活垃圾存放区建一个老年活动中心,这样必须把1200立方米的生活垃圾运走:
(1)假如每天能运x立方米,所需时间为y天,写出y与x之间的函数表达式;
(2)若每辆拖拉机一天能运12立方米,则5辆这样的拖拉机要用多少天才能运完?
(3)在(2)的情况下,运了8天后,剩下的任务要在不超过6天的时间内完成,那么至少需要增加多少辆这样的拖拉机才能按时完成任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在□ABCD中,AE是BC边上的高,将![]() 沿
沿![]() 方向平移,使点E与点C重合,得
方向平移,使点E与点C重合,得![]() .
.
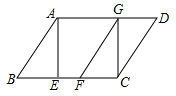
(1)求证:![]() ;
;
(2)若![]() ,当AB与BC满足什么数量关系时,四边形
,当AB与BC满足什么数量关系时,四边形![]() 是菱形?并说明理由.
是菱形?并说明理由.
注:(直角三角形中30°角所对直角边等于斜边的一半).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com