
【题目】已知抛物线y1=ax2+bx+c(ab≠0)经过原点,顶点为A.
(1)若点A的坐标是(﹣2,﹣4),
①求抛物线的解析式;
②把抛物线在第三象限之间的部分图象记为图象G,若直线y=﹣x+n与图象G有两个不同的交点,求n的取值范围;
(2)若直线y2=ax+b经过点A,当1<x<2时,比较y1与y2的大小.
【答案】(1)①y1=x2+4x;②﹣![]() <n<﹣2;(2)当a>0时,a(x﹣2)(x﹣1)<0,y1<y2;当a<0时,a(x﹣2)(x﹣1)>0,y1>y2.
<n<﹣2;(2)当a>0时,a(x﹣2)(x﹣1)<0,y1<y2;当a<0时,a(x﹣2)(x﹣1)>0,y1>y2.
【解析】
(1)①设抛物线的解析式为:y1=a(x+2)2﹣4,根据抛物线y1=ax2+bx+c(ab≠0)经过原点,得到0=4a﹣4,于是得到结论;
②在y1=x2+2x中,令y1=0,则x2+2x=0,得到抛物线与x轴的交点为:(﹣2,0),(0,0);解不等式得到n>﹣![]() ,当直线y=﹣x+n过点(﹣2,0),则n=﹣2,于是得到结论;
,当直线y=﹣x+n过点(﹣2,0),则n=﹣2,于是得到结论;
(2)将函数y1的解析式配方,即可找出其顶点坐标,将顶点坐标代入函数y2的解析式中,即可得出a、b的关系,再根据ab≠0,用a表示出b,两函数解析式做差,即可得出y1﹣y2=a(x﹣2)(x﹣1),根据x的取值范围可得出(x﹣2)(x﹣1)<0,分a>0或a<0两种情况考虑,即可得出结论.
(1)①∵顶点A(﹣2,﹣4),
∴设抛物线的解析式为:y1=a(x+2)2﹣4,
∵抛物线y1=ax2+bx+c(ab≠0)经过原点,
∴0=4a﹣4,
∴a=1,
∴抛物线的解析式为:y1=x2+4x;
②在y1=x2+2x中,令y1=0,则x2+2x=0,
解得:x1=0,x2=﹣2,
∴抛物线与x轴的交点为:(﹣2,0),(0,0);
解![]() 得,x2+3x﹣n=0,
得,x2+3x﹣n=0,
∵抛物线在第三象限之间的部分图象记为图象G,若直线y=﹣x+n与图象G有两个不同的交点,
∴△=9+4n>0,
∴n>﹣![]() ,
,
当直线y=﹣x+n过点(﹣2,0),则n=﹣2,
∴n的取值范围为:﹣![]() <n<﹣2;
<n<﹣2;
(2)∵抛物线y1=ax2+bx+c(ab≠0)经过原点,
∴y1=ax2+bx=a(x+![]() )2﹣
)2﹣![]() ,
,
∴函数y1的顶点为(﹣![]() ,﹣
,﹣![]() ),
),
∵函数y2的图象经过y1的顶点,
∴﹣![]() =a(﹣
=a(﹣![]() )+b,即b=﹣
)+b,即b=﹣![]() ,
,
∵ab≠0,
∴﹣b=2a,
∴b=﹣2a,
∴y1=ax2﹣2ax=ax(x﹣2),y2=ax﹣2a,
∴y1﹣y2=a(x﹣2)(x﹣1).
∵1<x<2,
∴x﹣2<0,x﹣1>0,(x﹣2)(x﹣1)<0.
当a>0时,a(x﹣2)(x﹣1)<0,y1<y2;
当a<0时,a(x﹣2)(x﹣1)>0,y1>y2.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:
【题目】已知:在△ABC中,AB=4,BC=5,CA=6.
(1)如果DE=10,那么当EF=________,FD=________时,△DEF∽△ABC;
(2)如果DE=10,那么当EF=________,FD=________时,△FDE∽△ABC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大学生创业团队抓住商机,购进一批干果分装成营养搭配合理的小包装后出售,每袋成本3元.试销期间发现每天的销售量y(袋)与销售单价x(元)之间满足一次函数关系,部分数据如表所示,其中3.5≤x≤5.5,另外每天还需支付其他各项费用80元.
销售单价x(元) | 3.5 | 5.5 |
销售量y(袋) | 280 | 120 |
(1)请直接写出y与x之间的函数关系式;
(2)如果每天获得160元的利润,销售单价为多少元?
(3)设每天的利润为w元,当销售单价定为多少元时,每天的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ACB中,∠C=90°,AC=BC,一直角三角板的直角顶角O在AB边的中点上,这块三角板绕O点旋转,两条直角边始终与AC、BC边分别相交于E、F,连接EF,则在运动过程中,△OEF与△ABC的关系是( )
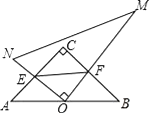
A. 一定相似 B. 当E是AC中点时相似
C. 不一定相似 D. 无法判断
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=![]() x2+
x2+ ![]() x+c与x轴的负半轴交于点A,与y轴交于点B,连结AB,点C(6,
x+c与x轴的负半轴交于点A,与y轴交于点B,连结AB,点C(6,![]() )在抛物线上,直线AC与y轴交于点D.
)在抛物线上,直线AC与y轴交于点D.
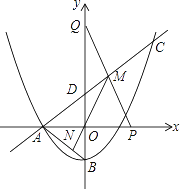
(1)求c的值及直线AC的函数表达式;
(2)点P在x轴正半轴上,点Q在y轴正半轴上,连结PQ与直线AC交于点M,连结MO并延长交AB于点N,若M为PQ的中点.
①求证:△APM∽△AON;
②设点M的横坐标为m,求AN的长(用含m的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,规定:抛物线![]() 的伴随直线为
的伴随直线为![]() .例如:抛物线
.例如:抛物线![]() 的伴随直线为
的伴随直线为![]() ,即y=2x﹣1.
,即y=2x﹣1.
(1)在上面规定下,抛物线![]() 的顶点坐标为 ,伴随直线为 ,抛物线
的顶点坐标为 ,伴随直线为 ,抛物线![]() 与其伴随直线的交点坐标为 和 ;
与其伴随直线的交点坐标为 和 ;
(2)如图,顶点在第一象限的抛物线![]() 与其伴随直线相交于点A,B(点A在点B的左侧),与x轴交于点C,D.
与其伴随直线相交于点A,B(点A在点B的左侧),与x轴交于点C,D.
①若∠CAB=90°,求m的值;

②如果点P(x,y)是直线BC上方抛物线上的一个动点,△PBC的面积记为S,当S取得最大值![]() 时,求m的值.
时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]() 的图像与
的图像与![]() 轴的一个交点为
轴的一个交点为![]()
![]() ,与
,与![]() 轴的交点为
轴的交点为![]() ,过
,过![]() 的直线为
的直线为![]() .
.
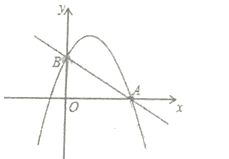
(1)求二次函数![]() 的解析式及点
的解析式及点![]() 的坐标;
的坐标;
(2)直接写出满足![]() 时,
时,![]() 的取值 ;
的取值 ;
(3)在两坐标轴上是否存在点![]() ,使得
,使得![]() 是以
是以![]() 为底边的等腰三角形?若存在,求出
为底边的等腰三角形?若存在,求出![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
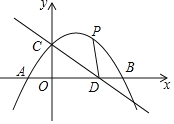
【题目】如图,抛物线交x轴于A、B两点![]() 点A在点B的左边
点A在点B的左边![]() ,交y轴于点C,直线
,交y轴于点C,直线![]() 经过点C与x轴交于点D,抛物线的顶点坐标为
经过点C与x轴交于点D,抛物线的顶点坐标为![]() .
.
![]() 请你直接写出CD的长及抛物线的函数关系式;
请你直接写出CD的长及抛物线的函数关系式;
![]() 求点B到直线CD的距离;
求点B到直线CD的距离;
![]() 若点P是抛物线位于第一象限部分上的一个动点,则当点P运动至何处时,恰好使
若点P是抛物线位于第一象限部分上的一个动点,则当点P运动至何处时,恰好使![]() ?请你求出此时的P点坐标.
?请你求出此时的P点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
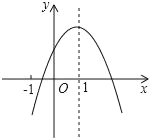
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图,有下列6个结论:
①abc<0;
②b<a﹣c;
③4a+2b+c>0;
④2c<3b;
⑤a+b<m(am+b),(m≠1的实数)
⑥2a+b+c>0,其中正确的结论的有_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com