
【题目】如图,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D,BE=3cm,AD=9cm.
求:(1)DE的长;
(2)若CE在△ABC的外部(如图),其它条件不变,DE的长是多少?

【答案】(1)DE= 6cm;(2)DE= 12cm.
【解析】试题分析:(1)由余角的性质,推出∠CBE=∠ECA,再依据全等三角形的判定定理“AAS”,推出△BEC和△CDA全等,然后即得BE=CD,CE=AD,再由BE=3cm,AD=9cm,结合图形即可推出DE=6cm,(2)根据余角的性质推出∠CBE=∠ACD,再依据全等三角形的判定定理“AAS”,推出△BEC和△CDA全等,然后即得BE=CD,CE=AD,再由BE=3cm,AD=9cm,结合图形即可推出DE=12cm.
试题解析:解:(1)∵∠ACB=90°,BE⊥CE,∴∠BCE+∠CBE=90°,∠BCE+∠ECA=90°,∴∠CBE=∠ECA,∠BEC=∠CDA.在△BEC和△CDA中,∵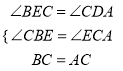 ,∴△BEC≌△CDA(AAS),∴BE=CD,CE=AD.∵BE=3cm,AD=9cm,∴CD=3cm,CE=9cm,∴DE=CE﹣CD=6cm.
,∴△BEC≌△CDA(AAS),∴BE=CD,CE=AD.∵BE=3cm,AD=9cm,∴CD=3cm,CE=9cm,∴DE=CE﹣CD=6cm.
(2)∵∠ACB=90°,BE⊥CE于E,AD⊥CE于D,∴∠BCE+∠CBE=90°,∠BCE+∠DCA=90°,∠BEC=∠CDA=90°,∴∠CBE=∠ACD.在△CBE和△ACD中,∵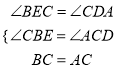 ,∴△CBE≌△ACD(AAS),∴BE=CD,CE=AD.∵BE=3cm,AD=9cm,∴DE=CD+CE=BE+AD=12cm.
,∴△CBE≌△ACD(AAS),∴BE=CD,CE=AD.∵BE=3cm,AD=9cm,∴DE=CD+CE=BE+AD=12cm.


科目:初中数学 来源: 题型:
【题目】阅读下面的文字,解答问题.
大家知道![]() 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此![]() 的小数部分我们不可能全部地写出来,但是由于1<
的小数部分我们不可能全部地写出来,但是由于1<![]() <2,所以
<2,所以![]() 的整数部分为1,将
的整数部分为1,将![]() 减去其整数部分1,差就是小数部分
减去其整数部分1,差就是小数部分![]() -1,根据以上的内容,解答下面的问题:
-1,根据以上的内容,解答下面的问题:
(1)![]() 的整数部分是 ,小数部分是 ;
的整数部分是 ,小数部分是 ;
(2)1+![]() 的整数部分是 ,小数部分是 ;
的整数部分是 ,小数部分是 ;
(3)若设2+![]() 整数部分是x,小数部分是y,求x-y的值.
整数部分是x,小数部分是y,求x-y的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场一种商品的进价为每件30元,售价为每件40元,每天可以销售48件,为尽快减少库存,商场决定降价促销.
(1)若该商品连续两次下调相同的百分率后售价降至每件32.4元,求两次下降的百分率;
(2)经调查,若该商品每降价0.5元,每天可多销售4件,那么每天要想获得510元的利润,每件应降价多少元?
(3)在(2)的条件下,每件商品的售价为多少元时,每天可获得最大利润?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】方程![]() 的解为
的解为![]()
![]() 的解为
的解为![]()
![]() 的解为
的解为![]() ;……根据发现的规律:
;……根据发现的规律:
(1)请写出第7个方程:___________,它的解为x1=____________ , x2=____________.
(2)请写出第(n-1)个方程:____________,它的解为x1=____________, x2=____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点分别为A(2,3),B(3,1),C(-2,-2).
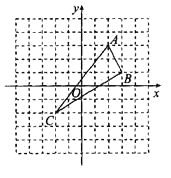
(1)请在图中作出△ABC关于y轴的轴对称图形△A′B′C′(A,B,C的对称点分别是A′,B′,C′),并直接写出A′,B′,C′的坐标.
(2)求△A′B′C′的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD为∠CAF的角平分线,BD=CD,∠DBC=∠DCB,∠DCA=∠ABD,过D作DE⊥AC于E,DF⊥AB交BA的延长线于F,则下列结论:①△CDE≌△BDF;②CE=AB+AE;③∠BDC=∠BAC;④∠DAF=∠CBD.其中正确的结论有( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是同一时刻学校里一棵树和旗杆的影子,如果树高为3米,测得它的影子长为1.2米,旗杆的高度为5米,则它的影子长为( ) 
A.4米
B.2米
C.1.8米
D.3.6米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在矩形ABCD中,对角线AC,BD相交于点O,E是CD中点,连结OE.过点C作CF∥BD交线段OE的延长线于点F,连结DF.求证: 
(1)△ODE≌△FCE;
(2)四边形ODFC是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的箱子里,装有黄、白、黑各一个球,它们除了颜色之外没有其他区别,随机从箱子里取出1个球,放回搅匀再取一次,请你用画树状图或列表的方法表示所有可能出现的结果,求两次取出的都是白球的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com