
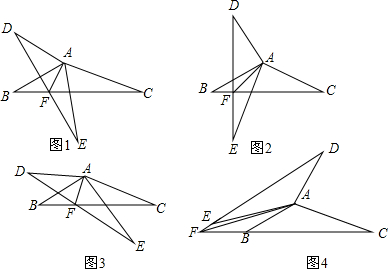
分析 (1)作AM⊥DE于M,AN⊥BC于N,如图1,由旋转的性质得∠DFB=60°,△ABC≌△ADE,则利用全等三角形的性质得AM=AN,于是根据角平分线定理的逆定理可判断AF平分∠DFC,即∠AFC=∠DFA-=60°,于是到∠AFB=2∠DFA=120°;
(2)当α=90°(如图2),根据旋转的性质得∠DFB=90°,同理可得AF平分∠DFC,即∠DFB=∠AFC=45°吗,则∠AFB=∠DFB+∠DFA=135°;
(3)若0°<α<120°(如图3),由旋转的性质得∠DFB=α,同理可得AF平分∠DFC,即∠DFA=∠AFC,则∠DFA=$\frac{1}{2}$(180°-α)=90°°-$\frac{1}{2}$α,所以∠AFB=∠DFB+∠DFA=90°+$\frac{1}{2}$α;
(4),如图4,根据旋转性质得∠PFC=α,利用邻补角定义得∠DFC=180°-α,同理可得AF平分∠DFC,即∠DFB=∠DFA,于是得到∠DFA=90°-$\frac{1}{2}$α
解答  解:(1)作AM⊥DE于M,AN⊥BC于N,如图1,
解:(1)作AM⊥DE于M,AN⊥BC于N,如图1,
∵△ABC绕点A顺时针旋转角度60°至△ADE,
∴∠DFB=60°,△ABC≌△ADE,
∴AM=AN,
∴AF平分∠DFC,即∠AFC=∠DFA,
而∠DFC=180°-60°=120°,
∴∠AFB=2∠DFA=120°;
(2)若α=90°(如图2),与(1)一样可得∠DFB=90°,AF平分∠DFC,即∠DFA=∠AFC,
∴∠DFA=45°
∴∠AFB=∠DFB+∠DFA=90°+45°=135°;
故答案为120°,135°;
(3)若0°<α<120°(如图3),∠AFB=90°+$\frac{1}{2}$α.理由如下:
∵△ABC绕点A顺时针旋转角度α至△ADE,
∴∠DFB=α,
与(1)一样可证明AF平分∠DFC,即∠DFA=∠AFC,
∴∠DFA=$\frac{1}{2}$(180°-α)=90°°-$\frac{1}{2}$α
∴∠AFB=∠DFB+∠DFA=α+90°-$\frac{1}{2}$α=90°+$\frac{1}{2}$α;
(4)、(3)中的猜想结论不成立.∠AFB=90°-$\frac{1}{2}$α.理由如下:
如图4,∵△ABC绕点A顺时针旋转角度α至△ADE,
∴∠PFC=α,
∴∠DFC=180°-α,
同理可得AF平分∠DFC,即∠DFA=∠AFC,
∴∠AFB=$\frac{1}{2}$(180°-α)=90°-$\frac{1}{2}$α
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了角平分线定理的逆定理.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 如图所示,在△ABC中,∠A=90°,D为BC的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,试探究线段BE,EF,FC之间的数量关系.
如图所示,在△ABC中,∠A=90°,D为BC的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,试探究线段BE,EF,FC之间的数量关系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
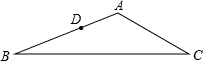 如图,在△ABC中,AB=12cm,BC=18cm,AC=9cm,D为AB上一点,BD=$\frac{2}{3}$AB,E是AC上的一点.若△ADE与△ABC相似,请你画出线段DE并求DE的长.
如图,在△ABC中,AB=12cm,BC=18cm,AC=9cm,D为AB上一点,BD=$\frac{2}{3}$AB,E是AC上的一点.若△ADE与△ABC相似,请你画出线段DE并求DE的长.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
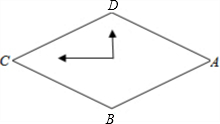 某课外小组设计了一个菱形挂钟.如图,菱形的边长为12厘米,时钟的中心在菱形的交点上,∠ADC=120°,数字3,6,9,12分别在四个顶点ABCD上,则数字1的位置与D点的距离为( )
某课外小组设计了一个菱形挂钟.如图,菱形的边长为12厘米,时钟的中心在菱形的交点上,∠ADC=120°,数字3,6,9,12分别在四个顶点ABCD上,则数字1的位置与D点的距离为( )| A. | 3厘米 | B. | 4厘米 | C. | 3$\sqrt{3}$厘米 | D. | 6厘米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC中,$\frac{AD}{DB}$=$\frac{AE}{EC}$=$\frac{1}{2}$,求$\frac{OE}{OB}$的值.
如图,△ABC中,$\frac{AD}{DB}$=$\frac{AE}{EC}$=$\frac{1}{2}$,求$\frac{OE}{OB}$的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com