
 ��ͼ��ʾ�����ı���ABCD�У�AD��BC����B=90�㣬AD=17cm��BC=20cm������P�ӵ�A������AD�������D��1cm/s���ٶ��˶�������Q�ӵ�C��ʼ��CB�������B��3cm/s���ٶ��˶�����P��Q�ֱ�ӵ�A�͵�Cͬʱ������������һ�㵽��˵�ʱ����һ����ֹ֮ͣ�˶���
��ͼ��ʾ�����ı���ABCD�У�AD��BC����B=90�㣬AD=17cm��BC=20cm������P�ӵ�A������AD�������D��1cm/s���ٶ��˶�������Q�ӵ�C��ʼ��CB�������B��3cm/s���ٶ��˶�����P��Q�ֱ�ӵ�A�͵�Cͬʱ������������һ�㵽��˵�ʱ����һ����ֹ֮ͣ�˶������� ����˶�ʱ��t����ʾ��AP��CQ��PD��BQ��
��1�����ı���PQCD��ƽ���ı��Σ��ó�PD=CQ������������⼴�ɣ�
��2�����ı���PQBA�Ǿ��Σ��ó�AP=BQ����������⼴�ɣ�
��3���ɣ�2�����ı���PQBA�������Σ��ó�DE=AB=AP=3�����ù��ɶ�����⼴�ɣ�
��� �⣺���˶�ʱ��Ϊt����AP=t��CQ=3t��
��PD=17-t��BQ=20-3t��
��1�����ı���PQCD��ƽ���ı��Σ���AD��BC��
��PD=CQ��
��17-t=3t��
��t=$\frac{17}{4}$��
������P�˶�$\frac{17}{4}$��ʱ���ı���PQCD��ƽ���ı��Σ�
��2�����ڣ�
���ɣ����ı���PQBA�Ǿ��Σ���AD��BC����B=90�㣬
��AP=BQ��
��t=20-3t��
��t=5��
�����˶�ʱ��Ϊ5��ʱ���ı���PQBA�Ǿ��Σ�
��3����ͼ��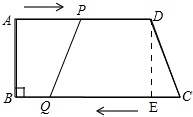
����D��DE��BC��
���ı���ADEB�Ǿ��Σ�
��DE=AB��BE=AD��
�ɣ�2����t=5ʱ���ı���PQBA�Ǿ��Σ�
��AP=t=5��
���ı���PQBA�������Σ�
��AB=AP=5��
��DE=AB=5��
��Rt��CDE��DE=4��CE=BC-BE=BC-AD=20-17=3��
���ݹ��ɶ����ã�CD=$\sqrt{D{E}^{2}+C{E}^{2}}$=$\sqrt{25+9}$=$\sqrt{34}$��
���� �������ı����ۺ��⣬��Ҫ������ƽ���ı��Σ����Σ������ε����ʣ����ɶ������Ȿ��Ĺؼ����÷��̵�˼�������⣮


 ��������ϵ�д�
��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{0.09}$=0.3 | B�� | $\sqrt{1\frac{7}{9}}$=$��\frac{4}{3}$ | C�� | $\sqrt{��-5��^{2}}$=-5 | D�� | -32��ƽ������-3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��AB�ǡ�O��ֱ��������DA��DB�ֱ�O�ڵ�E��C����AD=AB����DAB����ǣ�����EC��OE��OC��
��ͼ��AB�ǡ�O��ֱ��������DA��DB�ֱ�O�ڵ�E��C����AD=AB����DAB����ǣ�����EC��OE��OC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

| ��P����M�ľ��� | ��P����N�ľ��� | |
| ��P��M��N֮�� | x-��-5�� | -x+4 |
| ��P�ڵ�M��� | -5-x | 4-x |
| ��P�ڵ�N�Ҳ� | x-��-5�� | x-4 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com