
分析 (1)根据方程有实数根结合根的判别式,即可得出关于m的一元一次不等式,解之即可得出结论;
(2)利用根与系数的关系可得出x1+x2=2m+3、x1•x2=m2+2,结合x12+x22=31+x1x2即可得出关于m的一元二次方程,解之即可得出m的值.
解答 解:(1)∵方程x2-(2m+3)x+m2+2=0有实数根,
∴△=[-(2m+3)]2-4(m2+2)=12m+1≥0,
解得:m≥-$\frac{1}{12}$.
(2)∵方程x2-(2m+3)x+m2+2=0的两个根分别为x1、x2,
∴x1+x2=2m+3,x1•x2=m2+2,
∵x12+x22=31+x1x2,
∴$({x}_{1}+{x}_{2})^{2}$-2x1•x2=31+x1x2,即m2+12m-28=0,
解得:m1=2,m2=-14(舍去),
∴实数m的值为2.
点评 本题考查了根与系数的关系以及根的判别式,熟练掌握当一元二次方程有实数根时根的判别式△≥0是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
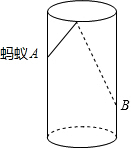 如图,透明的圆柱形容器(容器厚度忽略不计)的高为12cm,底面周长为10cm,在容器内壁离容器底部3cm的点B处有一饭粒,此时一只蚂蚁正好在容器外壁,且离容器上沿3cm的点A处,则蚂蚁吃到饭粒需爬行的最短路径是多少?
如图,透明的圆柱形容器(容器厚度忽略不计)的高为12cm,底面周长为10cm,在容器内壁离容器底部3cm的点B处有一饭粒,此时一只蚂蚁正好在容器外壁,且离容器上沿3cm的点A处,则蚂蚁吃到饭粒需爬行的最短路径是多少?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com