练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

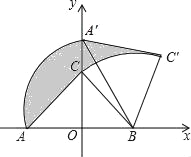
    【题目】如图，Rt△ABC中，∠ACB=90°，在以AB的中点O为坐标原点，AB所在直线为x轴建立的平面直角坐标系中，将△ABC绕点B顺时针旋转，使点A旋转至y轴的正半轴上的A′处，若AO=OB=2，则阴影部分面积为（　　）

    A. π B. π﹣1 C. +1 D.

    【答案】D

    【解析】分析：根据等腰直角三角形的性质求出AB，再根据旋转的性质可得，然后求出，再根据直角三角形两锐角互余求出即旋转角为60°，再根据S阴影=S扇形ABA′+S△A′BC′-S△ABC-S扇形CBC′=S扇形ABA′-S扇形CBC′，然后利用扇形的面积公式列式计算即可得解．

    详解：∵，AC=BC，

    ∴△ABC是等腰直角三角形，

    ∴

    ∵△ABC绕点B顺时针旋转点A在A′处，

    ∴BA′=AB，

    ∴BA′=2OB，

    ∴

    ∴

    即旋转角为

    S阴影=S扇形ABA′+S△A′BC′S△ABCS扇形CBC′,

    =S扇形ABA′S扇形CBC′,

    故选D.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

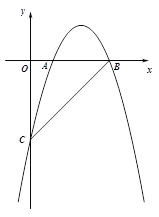
    【题目】（本题10分）如图，在平面直角坐标系xOy中，直线与y轴交于点C，与x轴交于点B，抛物线经过B、C两点，与x轴的正半轴交于另一点A，且OA ：OC="2" ：7．

    （1）求抛物线的解析式；

    （2）点D为线段CB上，点P在对称轴的右侧抛物线上，PD=PB，当tan∠PDB＝２，求P点的坐标；

    （3）在（2）的条件下，点Q（7，m）在第四象限内，点R在对称轴的右侧抛物线上，若以点P、D、Q、R为顶点的四边形为平行四边形，求点Q、R的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

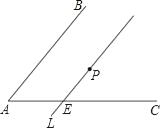
    【题目】如图，∠BAC内有一点P，过点P作直线l∥AB，交AC于E点．今欲在∠BAC的两边上各找一点Q、R，使得P为QR的中点，以下是甲、乙两人的作法：

    甲：①过P作直线l1∥AC，交直线AB于F点，并连接EF；

    ②过P作直线l2∥EF，分别交两直线AB、AC于Q、R两点，则Q、R即为所求．

    乙：①在直线AC上另取一点R，使得AE=ER；

    ②作直线PR，交直线AB于Q点，则Q、R即为所求．

    下列判断正确的是（　　）

    A. 两人皆正确 B. 两人皆错误

    C. 甲正确，乙错误 D. 甲错误，乙正确

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】嫦娥四号探测器于2019年1月3日，成功着陆在月球背面，通过“鹊桥”中继星传回了世界第一张近距离拍摄的月背影像图，开启了人类月球探测新篇章．当中继星成功运行于地月拉格朗日L2点时，它距离地球约1500000km．用科学记数法表示数1500000为( )

    A. 15×105 B. 1.5×106 C. 0.15×107 D. 1.5×105

    查看答案和解析>>

    科目：初中数学 来源： 题型：

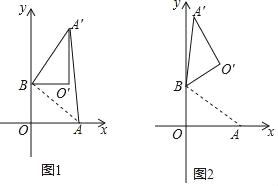
    【题目】在平面直角坐标系中，O为原点，点A（8，0），点B（0，6），把△ABO绕点B逆时针旋转得△A′B′O′，点A、O旋转后的对应点为A′、O′，记旋转角为α．

    （1）如图1，若α=90°，则AB=　 　，并求AA′的长；

    （2）如图2，若α=120°，求点O′的坐标；

    （3）在（2）的条件下，边OA上的一点P旋转后的对应点为P′，当O′P+BP′取得最小值时，直接写出点P′的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】甲、乙两车从A城出发匀速行驶至B城，在整个行驶过程中，甲、乙两车离开A城的距离y（km）与行驶的时间t（h）之间的函数关系如图所示．

    （1）求乙车离开A城的距离y关于t的函数解析式；

    （2）求乙车的速度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】请阅读下列材料：

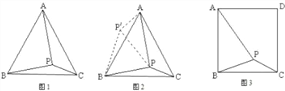
    问题：如图1，在等边三角形ABC内有一点P，且PA=2，PB=，PC=1、求∠BPC度数的大小和等边三角形ABC的边长．

    李明同学的思路是：将△BPC绕点B逆时针旋转60°，画出旋转后的图形（如图2），连接PP′，可得△P′PB是等边三角形，而△PP′A又是直角三角形（由勾股定理的逆定理可证），所以∠AP′B=150°，而∠BPC=∠AP′B=150°，进而求出等边△ABC的边长为，问题得到解决．

    请你参考李明同学的思路，探究并解决下列问题：如图3，在正方形ABCD内有一点P，且PA=，BP=，PC=1．求∠BPC度数的大小和正方形ABCD的边长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】【问题提出】

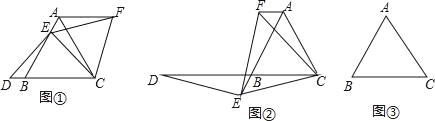
    如图①，已知△ABC是等腰三角形，点E在线段AB上，点D在直线BC上，且ED=EC，将△BCE绕点C顺时针旋转60°至△ACF连接EF

    试证明：AB=DB+AF

    【类比探究】

    （1）如图②，如果点E在线段AB的延长线上，其他条件不变，线段AB，DB，AF之间又有怎样的数量关系？请说明理由

    （2）如果点E在线段BA的延长线上，其他条件不变，请在图③的基础上将图形补充完整，并写出AB，DB，AF之间的数量关系，不必说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）用“*”表示一种新运算:对于任意正实数a,b,都有.例如,,那么15*27＝__；（2）定义一种运算*,其规则为:当a≥b时,a*b＝b3;当a＜b时,a*b＝b2.根据这个规则,方程3*x＝27的解是__.

    查看答案和解析>>

    同步练习册答案