
【题目】如图,在平面直角坐标系![]() 中,已知
中,已知![]() 的直角顶点
的直角顶点![]() ,斜边
,斜边![]() 在
在![]() 轴上,且点
轴上,且点![]() 的坐标为
的坐标为![]() ,点
,点![]() 是
是![]() 的中点,点
的中点,点![]() 是
是![]() 边上的一个动点,抛物线
边上的一个动点,抛物线![]() 过
过![]() ,
,![]() ,
,![]() 三点.
三点.
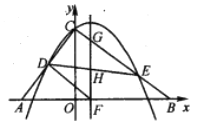
(1)当![]() 时,
时,
①求抛物线的解析式;
②平行于对称轴的直线![]() 与
与![]() 轴,
轴,![]() ,
,![]() 分别交于点
分别交于点![]() ,
,![]() ,
,![]() ,若以点
,若以点![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似,求点
相似,求点![]() 的值.
的值.
(2)以![]() 为等腰三角形顶角顶点,
为等腰三角形顶角顶点,![]() 为腰构造等腰
为腰构造等腰![]() ,且
,且![]() 点落在
点落在![]() 轴上.若在
轴上.若在![]() 轴上满足条件的
轴上满足条件的![]() 点有且只有一个时,请直接写出点
点有且只有一个时,请直接写出点![]() 的坐标.
的坐标.
【答案】(1)①![]() ;②
;②![]() 的值为
的值为![]() 或0;(2)
或0;(2)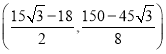 或
或![]() .
.
【解析】
(1)①先由A、C的坐标求出点D的坐标,由勾股定理求出AC,通过三角函数可求出DE,即可得到E点坐标,然后将D、E代入![]() 即可;②分
即可;②分![]() 和
和![]() 两种情况讨论,根据三角函数求解;
两种情况讨论,根据三角函数求解;
(2)分两种情况:①EG⊥AB,②以E为圆心DE为半径作圆,交AB延长线于M,过E作EH⊥AB于H, D、E、M三点共线时.
(1)①∵点![]() ,点
,点![]() ,
,
∴![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,
∵点![]() 是
是![]() 的中点,
的中点,
∴点![]() 的坐标为
的坐标为![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,即
,即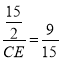 ,
,
∴![]() ,
,
∴![]() 的坐标为
的坐标为![]() ,即
,即![]() ,
,
把![]() 和D
和D![]() 代入
代入![]() ,
,
得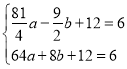 ,
,
解得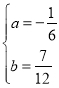 ,
,
∴抛物线的解析式为![]() .
.
②当![]() 时,可得
时,可得![]() ,
,
解得![]() ,
,
∴![]() ;
;
当![]() 时,可得
时,可得![]() ,
,
解得![]() ,
,
∴![]() .
.
综上所述,![]() 的值为
的值为![]() 或0.
或0.
(2)若在![]() 轴上满足条件的
轴上满足条件的![]() 点有且只有一个,则有两种情况,
点有且只有一个,则有两种情况,
第一种情况,EG⊥AB,如图,
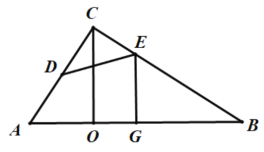
∠A+∠B=90°,∠B+∠BCO=90°,∠B+∠BEG=90°,
∴∠A=∠BCO=∠BEG,
∴△AOC∽△COB,△AOC∽△COB,
∴![]() ,
,![]() ,
,
∴![]() ,即
,即![]() ,
,
![]() ,即
,即![]() ,
,
设![]() ,则
,则![]() ,
,![]() ,
,
在直角三角形CDE中,![]() ,
,
∴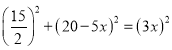 ,
,
解得![]() 或
或![]() (舍),
(舍),
![]() ,
,
由![]() ,
,![]() 得
得![]() ,
,![]() ,
,
∴![]() ,
,
∴E点坐标为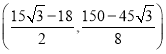 ,
,
第二种情况如图,以E为圆心DE为半径作圆,交AB延长线于M,过E作EH⊥AB于H, D、E、M三点共线时,
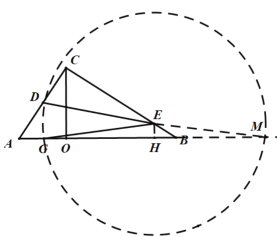
则E为DM的中点,
由D![]() 可知E的纵坐标为3,即EH=3,
可知E的纵坐标为3,即EH=3,
由题可知△EHB∽△COB,
∴![]() 即
即![]() ,
,
∴HB=4,OH=OB-HB=16-4=12,
∴E点坐标为![]() ,
,
∴答案为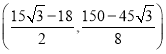 或
或![]() .
.


科目:初中数学 来源: 题型:
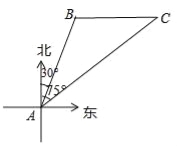
【题目】南海是我国的南大门,如图所示,某天我国一艘海监执法船在南海海域正在进行常态化巡航,在A处测得北偏东30°方向上,距离为20海里的B处有一艘不明身份的船只正在向正东方向航行,便迅速沿北偏东75°的方向前往监视巡查,经过一段时间后,在C处成功拦截不明船只,问我海监执法船在前往监视巡查的过程中行驶了多少海里(最后结果保留整数)?
![]()
![]() (参考数据:cos75°=0.2588,sin75°=0.9659,tan75°=3.732,
(参考数据:cos75°=0.2588,sin75°=0.9659,tan75°=3.732,![]() =1.732,
=1.732,![]() =1.414)
=1.414)
查看答案和解析>>
科目:初中数学 来源: 题型:
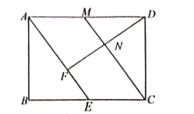
【题目】如图,在矩形![]() 中,点E为
中,点E为![]() 的中点,连接
的中点,连接![]() ,过点D作
,过点D作![]() 于点F,过点C作
于点F,过点C作![]() 于点N,延长
于点N,延长![]() 交
交![]() 于点M.
于点M.
(1)求证:![]()
(2)连接CF,并延长CF交AB于G
①若![]() ,求
,求![]() 的长度;
的长度;
②探究当![]() 为何值时,点G恰好为AB的中点.
为何值时,点G恰好为AB的中点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y关于x的二次函数y=x-bx+![]() b+b-5的图象与x轴有两个公共点.
b+b-5的图象与x轴有两个公共点.
(1)求b的取值范围;
(2)若b取满足条件的最大整数值,当m≤x≤![]() 时,函数y的取值范围是n≤y≤6-2m,求m,n的值;
时,函数y的取值范围是n≤y≤6-2m,求m,n的值;
(3)若在自变量x的值满足b≤x≤b+3的情况下,对应函数y的最小值为![]() ,求此时二次函数的解析式.
,求此时二次函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
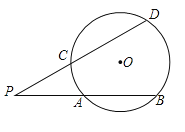
【题目】我们知道:顶点在圆上,并且两边都和圆相交的角叫做圆周角,一条弧所对的圆周角的度数等于它所对的圆心角度数的一半.类似地,我们定义:顶点在圆外,并且两边都和圆相交的角叫做圆外角.
(1)判断:图中有没有圆外角?如果有,请用字母表示出来.
(2)运用所学的数学知识,探究:圆外角的度数与它所夹的弧所对的圆心角的度数有什么关系?将你的发现,用文字表述出来,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【发现证明】
如图1,点E,F分别在正方形ABCD的边BC,CD上,∠EAF=45°,试判断BE,EF,FD之间的数量关系.
小聪把△ABE绕点A逆时针旋转90°至△ADG,通过证明△AEF≌△AGF;从而发现并证明了EF=BE+FD.
【类比引申】
(1)如图2,点E、F分别在正方形ABCD的边CB、CD的延长线上,∠EAF=45°,连接EF,请根据小聪的发现给你的启示写出EF、BE、DF之间的数量关系,并证明;
【联想拓展】
(2)如图3,如图,∠BAC=90°,AB=AC,点E、F在边BC上,且∠EAF=45°,若BE=3,EF=5,求CF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年 3 月 12 日植树节期间, 学校预购进 A、B 两种树苗,若购进 A种树苗 3 棵,B 种树苗 5 棵,需 2100 元,若购进 A 种树苗 4 棵,B 种树苗 10棵,需 3800 元.
(1)求购进 A、B 两种树苗的单价;
(2)若该单位准备用不多于 8000 元的钱购进这两种树苗共 30 棵,求 A 种树苗至少需购进多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】[问题]小明在学习时遇到这样一个问题:求不等式x3+3x2﹣x﹣3>0的解集.
他经历了如下思考过程:
[回顾]
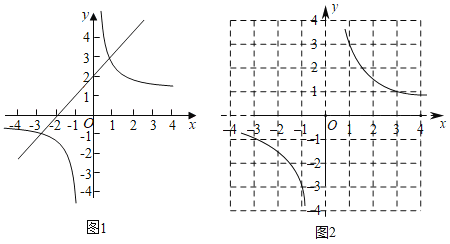
(1)如图1,在平面直角坐标系xOy中,直线y1=ax+b与双曲线y2=![]() 交于A (1,3)和B(﹣3,﹣1),则不等式ax+b>
交于A (1,3)和B(﹣3,﹣1),则不等式ax+b>![]() 的解集是 .
的解集是 .
[探究]将不等式x3+3x2﹣x﹣3>0按条件进行转化:
当x=0时,原不等式不成立;
当x>0时,不等式两边同除以x并移项转化为x2+3x﹣1>![]() ;
;
当x<0时,不等式两边同除以x并移项转化为x2+3x﹣1<![]() .
.
(2)构造函数,画出图象:
设y3=x2+3x﹣1,y4=![]() ,在同一坐标系中分别画出这两个函数的图象;
,在同一坐标系中分别画出这两个函数的图象;
双曲线y4=![]() 如图2所示,请在此坐标系中画出抛物线y=x2+3x﹣1.(不用列表)
如图2所示,请在此坐标系中画出抛物线y=x2+3x﹣1.(不用列表)
(3)确定两个函数图象公共点的横坐标:
观察所画两个函数的图象,猜想并通过代入函数解析式验证可知:满足y3=y4的所有x的值为 .
[解决]
(4)借助图象,写出解集:
结合“探究”中的讨论,观察两个函数的图象可知:不等式x3+3x2﹣x﹣3>0的解集为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com