
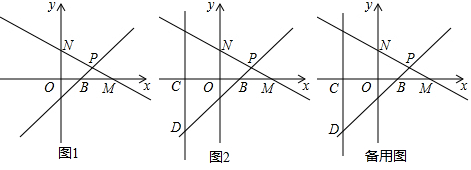
���� ��1������ֱ��y=-$\frac{1}{2}$x+2��ֱ��y=x+m�ཻ�ڵ�P�������������̽��x=$\frac{4-2m}{3}$��y=$\frac{4+m}{3}$���ٸ��ݵ�P�ڵ�һ���ޣ��ó�����ʽ���ɣ�
��2���ȵó���M�����꣬�ٵó���B�����꣬����ֱ��y=x+m�У����m��ֵ�����������飬�ó���P�����꼴�ɣ�
��3�����ݵ�M������ó���ԳƵ�C�����꣬�ٷ�OAΪ�ߺ�OAΪ�Խ������������ɣ�
��4���������⻭��ͼ�Σ����ɵó�d3��ֵ��
��� �⣺��1����Ϊֱ��y=-$\frac{1}{2}$x+2��ֱ��y=x+m�ཻ��P��
�ɵã�$\left\{\begin{array}{l}{y=-\frac{1}{2}x+2}\\{y=x+m}\end{array}\right.$��
��ã�x=$\frac{4-2m}{3}$��y=$\frac{4+m}{3}$��
���Ե�P������Ϊ����$\frac{4-2m}{3}$��$\frac{4+m}{3}$����
��Ϊ��P�ڵ�һ���ޣ��ɵã�$\left\{\begin{array}{l}{\frac{4-2m}{3}��0}\\{\frac{4+m}{3}��0}\end{array}\right.$��
��ã�-4��m��2��
����m��ȡֵ��ΧΪ��-4��m��2��
��2����Ϊֱ��y=-$\frac{1}{2}$x+2��x�ύ��M�㣬��ͼ1��
��y=0�ֱ�������ʽ�У��ɵã���M��4��0����
�ߵ�M��4��0������O������Ϊ��0��0����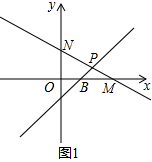
��BΪOM���е㣬�ɵõ�B������Ϊ��2��0����
��B��2��0����y=x+m�ϣ�
��ѵ�B���������ֱ��y=x+m�У��ɵã�2+m=0��
��ã�m=-2
��ֱ�ߵĽ���ʽΪ��y=x-2��
����ֱ�߽���ΪP��
������������ã�$\left\{\begin{array}{l}{y=-\frac{1}{2}x+2}\\{y=x-2}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{x=\frac{8}{3}}\\{y=\frac{2}{3}}\end{array}\right.$��
��P����������$\frac{8}{3}$��$\frac{2}{3}$����
��3���ߵ�M������Ϊ��4��0������M����ԭ��ĶԳƵ�ΪC����ͼ2��
��ɵã���C������Ϊ����-4��0����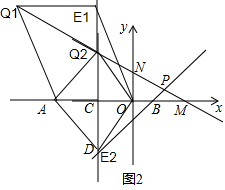
��ɵ�ֱ�ߵĽ���ʽΪ��x=-4���ҿɵ�A��-8��0����
��OA=8��
�ٵ�OAΪ��ʱ��
��MC=8��
��EQ$\underline{\underline{||}}$OA=8��
��Q����x=-4��࣬��EQ=8��
��xQ=-4-8=-12��
��x=-12����$y=-\frac{1}{2}x+2=8$��
��Q��-12��8����E��-4��8����
�ڵ�OAΪ�Խ��ߣ�
��CA=CO��
��CE=CQ��
��Q��-4��4����
�ɵã�E��-4��-4����
����������E1��-4��8����E2��-4��-4������
��4�����ڣ��籸��ͼ��ʾ��ֱ��l1��l2��l3��l4���ڣ���ʹ��${d_1}={d_2}=\frac{d_3}{2}$����d3��ֵ�ֱ�Ϊ��$2\sqrt{2}$��$6\sqrt{2}$��$\frac{{6\sqrt{10}}}{5}$��$\frac{{6\sqrt{10}}}{5}$����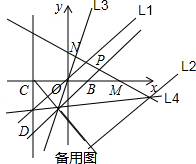
���� ���⿼��һ�κ������ۺ�Ӧ�ã��ؼ����г�����ʽ�����ô���ϵ�����ó�����ʽ��ע���뷽������ۺ����ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
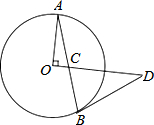 ��ͼ��AB��ԲO���ң�OA��OD��AB��OD�ཻ�ڵ�C����CD=BD��
��ͼ��AB��ԲO���ң�OA��OD��AB��OD�ཻ�ڵ�C����CD=BD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
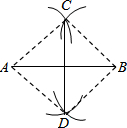 ��ͼ���ϴ������߶�AB�Ĵ�ֱƽ����ʱ���������������ģ��ֱ���A��BΪԲ�ģ�����$\frac{1}{2}$AB�ij�Ϊ�뾶��������������C��D����ֱ��CD��Ϊ������������ͼ������֪�ı���ADBCһ���ǣ�������
��ͼ���ϴ������߶�AB�Ĵ�ֱƽ����ʱ���������������ģ��ֱ���A��BΪԲ�ģ�����$\frac{1}{2}$AB�ij�Ϊ�뾶��������������C��D����ֱ��CD��Ϊ������������ͼ������֪�ı���ADBCһ���ǣ�������| A�� | ���� | B�� | ���� | C�� | ������ | D�� | �������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2}$ | B�� | $\frac{1}{3}$ | C�� | $\frac{1}{4}$ | D�� | $\frac{1}{6}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
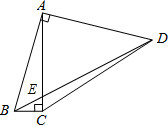 ��ͼ���ı���ABCD�У��Խ��߽��ڵ�E����BAD=��ACB=90�㣬AB=AD����tan��ABC=4��EC=1����BE=$\frac{\sqrt{34}}{3}$��
��ͼ���ı���ABCD�У��Խ��߽��ڵ�E����BAD=��ACB=90�㣬AB=AD����tan��ABC=4��EC=1����BE=$\frac{\sqrt{34}}{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
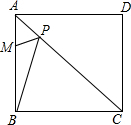 ��֪������ABCD��һ���Խ��߳�Ϊ6��M�DZ�AB��һ���㣬��AM��MB=1��2��P�ǶԽ���AC�ϵ�һ�����㣬��PM+PB����Сֵ=2$\sqrt{5}$��
��֪������ABCD��һ���Խ��߳�Ϊ6��M�DZ�AB��һ���㣬��AM��MB=1��2��P�ǶԽ���AC�ϵ�һ�����㣬��PM+PB����Сֵ=2$\sqrt{5}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com