
����Ŀ��������ѧ������Ҫ�õ���ѧ���������༶�������幺�С����ȥ�ľߵ깺����2��A�ͼ�������3��B�ͼ�������������90Ԫ����������1��A�ͼ�������2��B�ͼ�������������55Ԫ��ÿ�����ּ��������ۼ۶����䣩
��1����A�ͼ�������B�ͼ��������ۼ۷ֱ���ÿ������Ԫ��
��2����ͳ�ƣ����ڻ��蹺�����ּ�������40�����蹺��A�ͼ�����t���������ܷ���wԪ�������w����t�ĺ�����ϵʽ��
��3��Ҫ��B�ͼ�����������������A�ͼ�������2���������һ�ֹ�����ʹ�����ܷ�����ͣ�
���𰸡���1��A�ͼ������ۼ�Ϊÿ��15Ԫ��B�ͼ������ۼ�Ϊÿ��20Ԫ��2��W=-5t+800��3������A�ͼ�����13����B�ͼ�����27��ʱ��������ͣ���ͷ���Ϊ735Ԫ
�������������������1����A�ͼ��������ۼ�Ϊÿ��xԪ��B�ͼ��������ۼ�Ϊÿ��yԪ�����ݡ�������2��A�ͼ�������3��B�ͼ�������������90Ԫ����������1��A�ͼ�������2��
B�ͼ�������������55Ԫ�������ɵõ�����x��y�Ķ�Ԫһ�η����飬��֮���ɣ�
��2���蹺��A�ͼ�����t���������ܷ���wԪ������B�ͼ�������40-t�����������ܼ�=���ۡ��������������ɵõ�w����t�ĺ�������ʽ��
��3����B�ͼ�����������������A�ͼ�������2�������ɵó�����t��һԪһ�β���ʽ����֮������t��ȡֵ��Χ��������һ�κ��������ʿɽ����ֵ����.
�����������1����A�ͼ�������ۼ�Ϊÿ��xԪ��b�ͼ�����ۼ�Ϊÿ��ΪyԪ������
����ã� ![]() �����
�����![]()
��A�ͼ������ۼ�Ϊÿ��15Ԫ��B�ͼ������ۼ�Ϊÿ��20Ԫ
�蹺��A�ͼ����t���������ܷ���wԪ������B�ͼ������40-t����
W=15t+20��40-t��=-5t+800
��40-t��2t����t��![]()
W=-5t+800����-5��0������t���������С
��tΪ��������t=13ʱ��wmin=-5x13+800=735Ԫ
�𣺹���A�ͼ�����13����B�ͼ�����27��ʱ��������ͣ���ͷ���Ϊ735Ԫ


 ��������ܸ�ϰϵ�д�
��������ܸ�ϰϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾��Ͷ�ʿ���A��B�����²�Ʒ����Ϣ��ͨ�����еõ�������Ϣ��
��Ϣһ�����Ͷ��A�ֲ�Ʒ����������![]() ����Ԫ����Ͷ�ʽ��x����Ԫ��֮������������������ϵ��
����Ԫ����Ͷ�ʽ��x����Ԫ��֮������������������ϵ�� ![]() ��
��
��Ϣ�������Ͷ��B�ֲ�Ʒ����������![]() ����Ԫ����Ͷ�ʽ��x����Ԫ��֮��������κ�����ϵ��
����Ԫ����Ͷ�ʽ��x����Ԫ��֮��������κ�����ϵ�� ![]() ��
��
���ݹ�˾��Ϣ�����棬 ![]() ��
��![]() ����Ԫ����Ͷ�ʽ��x����Ԫ���IJ��ֶ�Ӧֵ���±���ʾ��
����Ԫ����Ͷ�ʽ��x����Ԫ���IJ��ֶ�Ӧֵ���±���ʾ��
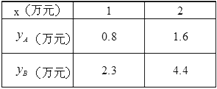
��1����գ� ![]() = ��
= �� ![]() = ��
= ��
��2�������˾��Ͷ��20��Ԫͬʱ����A��B�����²�Ʒ���蹫˾����õ�������ΪW����Ԫ����B�ֲ�Ʒ��Ͷ�ʽ��Ϊx����Ԫ������A�ֲ�Ʒ��Ͷ�ʽ��Ϊ_________��Ԫ�������W��x֮��ĺ�����ϵʽ��
��3���������һ���ڣ�2���й�˾�ܻ������������Ͷ�ʷ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͳ��2015��������ʵ�ֵ���������ֵ8011.5��Ԫ�����ɱȼ۸���㣬������������8%����8011.5���ÿ�ѧ��������ʾ�ǣ� ��
A.8011.5��108
B.801.15��109
C.8.0115��1010
D.8.0115��1011
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�AD=5��AB=8����EΪ����DC��һ�����㣬�ѡ�ADE��ֱ��AE�۵�������D�Ķ�Ӧ��F�պ������߶�AB�Ĵ�ֱƽ������ʱ����DE�ij�Ϊ________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���P��3����2������y��ĶԳƵ��� �� ����ԭ��ĶԳƵ��� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������ͨ3������2014��12��23�տ������裬Ԥ��2020��ȫ�߿�ͨ��3����ȫ��32.83ǧ�ף�32.83ǧ���ÿ�ѧ��������ʾΪ�� ��
A.3.283��104��
B.32.83��104��
C.3.283��105��
D.3.283��103��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��̽�����о���
����1����ͼ��a����������ķ���������ֱ��������������Ƕ�����ת90�����ã�����
��BAE��90�㣬���ı���ACFD��һ�������Σ�����������ı���ABFE�����ȣ����ı���ABFE�������Rt��BAE��Rt��BFE�����֮�ͣ�����ͼʾд��֤�����ɶ����Ĺ��̣�
����2����ͼ��b����������ķ�������������ȫ�ȵ�Rt��BEA��Rt��ACDƴ�ɵģ����ܸ���ͼʾ��дһ��֤�����ɶ����ķ�����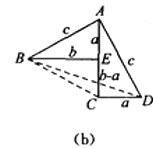
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ϵ�з���һ����OABC����֪��ABC=60�㣬��B��y���ϣ�OA=1���Ƚ�����OABC��x���������������ת��ÿ�η�ת60�㣬������ת2017�Σ���B���������ΪB1��B2��B3��������B2017������Ϊ��������

A. ��1345,0�� B. ��1345.5��![]() �� C. ��1345��
�� C. ��1345��![]() �� D. ��1345.5��0��
�� D. ��1345.5��0��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com