
分析 (1)按照用水量的多少进行分类:当0≤x≤10时,根据水费=用水单价×用水量即可得出y关于x的函数关系式;当10<x时,根据水费=10×0.8+(用水量-10)×1.6即可得出y关于x的函数关系式,联立二者即可得出结论;
(2)由(1)的结论可知当当0≤x≤10时,y≤8,由此可知小明家5月用水超过10吨,将y=11.2代入到y=1.6x-8中,求出x即可得出结论.
解答 解:(1)当0≤x≤10时,y=0.8x;
当10<x时,y=10×0.8+(x-10)×1.6=1.6x-8.
∴每月水费y元与每月用水量x立方米之间的函数关系式为y=$\left\{\begin{array}{l}{0.8x(0≤x≤10)}\\{1.6x-8(10<x)}\end{array}\right.$.
(2)∵当0≤x≤10时,y=0.8x≤10×0.8=8,且11.2>8,
∴10<x.
令y=1.6x-8中y=11.2,则11.2=1.6x-8,
解得:x=12.
答:小明家5月份水费为11.2元,他家用了12立方米的水.
点评 本题考查了一次函数的应用,解题的关键是:(1)根据数量关系找出函数关系式;(2)代入y=11.2,求出y值.本题属于基础题,难度不大,解决该题型题目时,根据数量关系找出函数关系式是关键.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:解答题
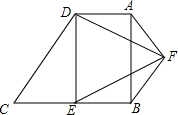 如图,在四边形ABCD中,AD∥BC,∠ABC=90°,∠C=60°,E是BC的中点,BC=2AD=$2\sqrt{3}$,△DEF是等边三角形,连结BF、AF.
如图,在四边形ABCD中,AD∥BC,∠ABC=90°,∠C=60°,E是BC的中点,BC=2AD=$2\sqrt{3}$,△DEF是等边三角形,连结BF、AF.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 矩形 | B. | 菱形 | C. | 正方形 | D. | 梯形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com