
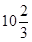 m,入水处与池边的距离为4m, 同时,运动员在距水面高度为5m以前,必须完成规定的翻腾动作,并调整好入水姿势,否则就会出现失误.
m,入水处与池边的距离为4m, 同时,运动员在距水面高度为5m以前,必须完成规定的翻腾动作,并调整好入水姿势,否则就会出现失误.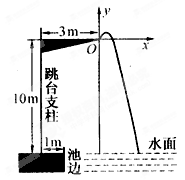
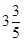 ,问:此次跳水会不会失误?通过计算说明理由.
,问:此次跳水会不会失误?通过计算说明理由.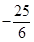 x2+
x2+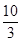 x;(2)此次试跳会出现失误,理由见解析.
x;(2)此次试跳会出现失误,理由见解析.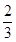 .
.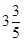 m时,距水面的高度是否小于5,若小于5,则会出现失误;若大于或等于5则不会失误.
m时,距水面的高度是否小于5,若小于5,则会出现失误;若大于或等于5则不会失误.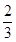 .
.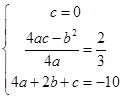 ,
,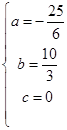 或
或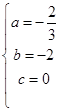 ,
,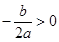 ,
,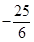 ,b=
,b=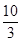 ,c=0.
,c=0.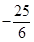 x2+
x2+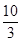 x;
x;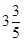 m时的纵坐标即可.
m时的纵坐标即可.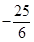 )×(
)×(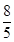 )2+
)2+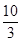 ×
×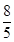 =
=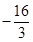 ,
,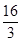 =
=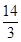 <5.
<5.

科目:初中数学 来源:不详 题型:解答题
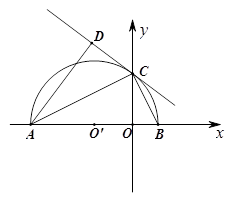
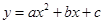 过A、B、C三点,AB=10,tan∠CAD=
过A、B、C三点,AB=10,tan∠CAD=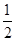 .
.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 与
与 轴相交于A、B两点,与
轴相交于A、B两点,与 轴相交于点C,若已知B点的坐标为B(8,0).
轴相交于点C,若已知B点的坐标为B(8,0).
 轴,求MN的最大值;
轴,求MN的最大值;查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 轴建立直角坐标系,桥洞上沿形状恰好是抛物线
轴建立直角坐标系,桥洞上沿形状恰好是抛物线 的图像.桥洞两侧壁上各有一盏距离水面4米高的景观灯.请求出这两盏景观灯间的水平距离.
的图像.桥洞两侧壁上各有一盏距离水面4米高的景观灯.请求出这两盏景观灯间的水平距离.

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.向上平移2个单位 | B.向左平移2个单位 |
| C.向下平移4个单位 | D.向右平移2个单位 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com