
【题目】图①为北斗七星的位置图,图②将北斗七星分别标为A,B,C,D,E,F,G,将A,B,C,D,E,F顺次首尾连接,若AF恰好经过点G,且AF∥DE,∠B=∠C+10°,∠D=∠E=105°.
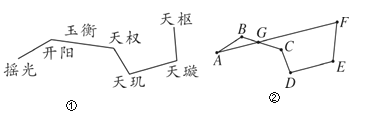
(1)求∠F的度数;
(2)计算∠B-∠CGF的度数是______;(直接写出结果)
(3)连接AD,∠ADE与∠CGF满足怎样数量关系时,BC∥AD,并说明理由.
【答案】(1)75°(2)115°(3)当∠ADE+∠CGF=180°时,BC∥AD
【解析】
(1)根据平行线的判定定理进行作答.即由AF∥DE,得到∠F+∠E=180°,因此∠F=75![]() .(2)延长DC交AF于点K. 根据角的变换,得到∠B-∠CGF=115°.(3)根据平行线的判定定理及性质进行作答.即由AF∥DE,得到∠GAD+∠ADE=180°,∠ADE+∠CGF=180°.再结合角的变换,得到∠GAD=∠CGF.所以,BC∥AD.
.(2)延长DC交AF于点K. 根据角的变换,得到∠B-∠CGF=115°.(3)根据平行线的判定定理及性质进行作答.即由AF∥DE,得到∠GAD+∠ADE=180°,∠ADE+∠CGF=180°.再结合角的变换,得到∠GAD=∠CGF.所以,BC∥AD.
(1)∵AF∥DE,
∴∠F+∠E=180°,
∴∠F=180°-105°=75°.
(2)如答图,延长DC交AF于点K.
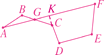
可得∠B-∠CGF=∠C+10°-∠CGF=∠GKC+10°=∠D+10°=115°.
(3)当∠ADE+∠CGF=180°时,BC∥AD,理由如下:
∵AF∥DE,
∴∠GAD+∠ADE=180°,∠ADE+∠CGF=180°,
∴∠GAD=∠CGF,∴BC∥AD.


科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点E、F分别是AC,BC的中点,直线EF与⊙O交于G、H两点,若⊙O的半径为7,则GE+FH的最大值为( )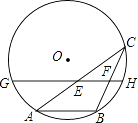
A.10.5
B.7 ![]() -3.5
-3.5
C.11.5
D.7 ![]() -3.5
-3.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=(m+1)x+2m-6.
(1)若函数图象过(-1,2),求此函数的解析式;
(2)若函数图象与直线y=2x+5平行,求其函数的解析式;
(3)求满足(2)条件的直线与直线y=-3x+1的交点,并求这两条直线与y轴所围成的三角形面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读以下材料:
对数的创始人是苏格兰数学家纳皮尔(J.Nplcr,1550﹣1617年),纳皮尔发明对数是在指数书写方式之前,直到18世纪瑞士数学家欧拉(Evlcr,1707﹣1783年)才发现指数与对数之间的联系.
对数的定义:一般地,若ax=N(a>0,a≠1),那么x叫做以a为底N的对数,记作:x=logaN.比如指数式24=16可以转化为4=log216,对数式2=log525可以转化为52=25.
我们根据对数的定义可得到对数的一个性质:loga(MN)=logaM+logaN(a>0,a≠1,M>0,N>0);理由如下:
设logaM=m,logaN=n,则M=am,N=an
∴MN=aman=am+n,由对数的定义得m+n=loga(MN)
又∵m+n=logaM+logaN
∴loga(MN)=logaM+logaN
解决以下问题:
(1)将指数43=64转化为对数式_____;
(2)证明loga![]() =logaM﹣logaN(a>0,a≠1,M>0,N>0)
=logaM﹣logaN(a>0,a≠1,M>0,N>0)
(3)拓展运用:计算log32+log36﹣log34=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,横、纵坐标都为整数的点称为整点.如图,从内向外依次为第![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 个正方形(实线),若整点
个正方形(实线),若整点![]() 在第
在第![]() 个正方形的边上,则
个正方形的边上,则![]() ,
,![]() ,
,![]() 之间满足的数量关系为_______.
之间满足的数量关系为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点C出发,按C→B→A的路径,以2cm每秒的速度运动,设运动时间为t秒,当t为___________时,△ACP是等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】工人师傅做铝合金窗框分下面三个步骤进行:
(1)先截出两对符合规格的铝合金窗料(如图①),使AB=CD,EF=GH;
(2)摆放成如图②的四边形,则这时窗框的形状是______形,根据的数学原理是:_______________________;
(3)将直角尺靠紧窗框的一个角(如图③),调整窗框的边框,当直角尺的两条直角边与窗框无缝隙时(如图④),说明窗框合格,这时窗框是_______形,根据的数学原理是:_____________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】第1个等式:1-![]() =
=![]() ×
×![]()
第2个等式:(1-![]() )(1-
)(1-![]() )=
)=![]() ×
×![]()
第3个等式:(1-![]() )(1-
)(1-![]() )(1-
)(1-![]() )=
)=![]() ×
×![]()
第4个等式:(1-![]() )(1-
)(1-![]() )(1-
)(1-![]() )(1-
)(1-![]() )=
)=![]() ×
×![]()
第5个等式:(1-![]() )(1-
)(1-![]() )(1-
)(1-![]() )(1-
)(1-![]() )(1-
)(1-![]() )=
)=![]() ×
×![]()
······
(1) 写出第6个等式;
(2) 写出第n个等式(用含n的等式表示),并予以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,EF切⊙O于点D,过点B作BH⊥EF于点H,交⊙O于点C,连接BD. 
(1)求证:BD平分∠ABH;
(2)如果AB=12,BC=8,求圆心O到BC的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com