
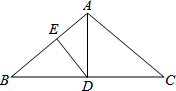
 如图,在△ABC中,AB=4,AD是△ABC的平分线,DE⊥AB于E,且DE=2
如图,在△ABC中,AB=4,AD是△ABC的平分线,DE⊥AB于E,且DE=2分析 (1)根据作线段的垂直平分线这个基本作图求解;
(2)根据线段垂直平分线的性质得FA=FD,则∠FAD=∠FDA,加上∠EAD=∠FAD,所以∠EAD=∠FDA,于是可判断DF∥AB;
(3)DF=AF=x,则FC=AC-x,先证明△CDF∽△CBA,利用相似比可求出AC=$\frac{4x}{4-x}$,再利用角平分线的性质得到点D到AB和AC的距离都等于2,则可根据三角形面积公式得到y=$\frac{1}{2}$•2•4+$\frac{1}{2}$•2•$\frac{4x}{4-x}$=$\frac{16}{4-x}$,由于当x最小时,4-x最大,y最小,根据垂线段最短得x的最小值为2,然后计算y的最小值.
解答 (1)解:如图,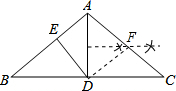
(2)证明:∵作AD的垂直平分线交AC于F,
∴FA=FD,
∴∠FAD=∠FDA,
而AD是△ABC的平分线,
∴∠EAD=∠FAD,
∴∠EAD=∠FDA,
∴DF∥AB;
(3)解:DF=AF=x,则CF=AC-x,
∵DF∥AB,
∴△CDF∽△CBA,
∴$\frac{CF}{AB}$=$\frac{CF}{CA}$,即$\frac{x}{4}$=$\frac{AC-x}{AC}$,解得AC=$\frac{4x}{4-x}$,
∵AD平分∠BAC,
∴点D到AB和AC的距离都等于2,
∴y=S△ADB+S△ADC
=$\frac{1}{2}$•2•4+$\frac{1}{2}$•2•$\frac{4x}{4-x}$
=$\frac{16}{4-x}$,
∵当x最小时,4-x最大,则y最小,
∴当DF⊥AC时,x最小,此时x=2,
∴y的最小值=$\frac{16}{4-2}$=8.
点评 本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了角平分线、线段的垂直平分线的性质和相似三角形的判定与性质.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | ${x^2}+3x-4=x({x+3-\frac{4}{x}})$ | B. | (x+2)(x-2)=x2-4 | ||
| C. | x2-4+3x=(x+2)(x-2)+3x | D. | $-{x^2}+x-\frac{1}{4}=-{({x-\frac{1}{2}})^2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
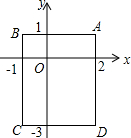 如图,在平面直角坐标系xoy中,已知点A(2,1)、B(-1,1)、C(-1,-3)、D(2,-3),把一根长为2015个单位长度没有弹性的细线(线的粗细忽略不计)的一端固定在D处,并按D→C→B→A→D…的规律紧绕在四边形ABCD的边上,则细线的另一端所在位置的点的坐标为(2,-2).
如图,在平面直角坐标系xoy中,已知点A(2,1)、B(-1,1)、C(-1,-3)、D(2,-3),把一根长为2015个单位长度没有弹性的细线(线的粗细忽略不计)的一端固定在D处,并按D→C→B→A→D…的规律紧绕在四边形ABCD的边上,则细线的另一端所在位置的点的坐标为(2,-2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
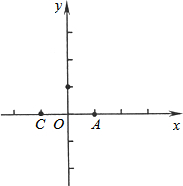 在平面直角坐标系中,点A,B,C的坐标分别为(1,0),(0,1),(-1,0).一个电动玩具从坐标原点O出发,第一次跳跃到点P1,使得点P1与点O关于点A成中心对称;第二次跳跃到点P2,使得点P2与点P1关于点B成中心对称;第三次跳跃到点P3,使得点P3与点P2关于点C成中心对称;第四次跳跃到点P4,使得点P4与点P3关于点A成中心对称;第五次跳跃到点P5,使得点P5与点P4关于点B成中心对称;…照此规律重复下去.则点P3的坐标为(0,-2);点Pn在y轴上,则点Pn的坐标为(0,0)或(0,-2).
在平面直角坐标系中,点A,B,C的坐标分别为(1,0),(0,1),(-1,0).一个电动玩具从坐标原点O出发,第一次跳跃到点P1,使得点P1与点O关于点A成中心对称;第二次跳跃到点P2,使得点P2与点P1关于点B成中心对称;第三次跳跃到点P3,使得点P3与点P2关于点C成中心对称;第四次跳跃到点P4,使得点P4与点P3关于点A成中心对称;第五次跳跃到点P5,使得点P5与点P4关于点B成中心对称;…照此规律重复下去.则点P3的坐标为(0,-2);点Pn在y轴上,则点Pn的坐标为(0,0)或(0,-2).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
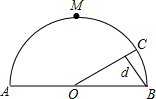 如图是自行车骑行训练场地的一部分,半圆O的直径AB=100,在半圆弧上有一运动员C从B点沿半圆周匀速运动到M(最高点),此时由于自行车故障原地停留了一段时间,修理好继续以相同的速度运动到A点停止.设运动时间为t,点B到直线OC的距离为d,则下列图象能大致刻画d与t之间的关系是( )
如图是自行车骑行训练场地的一部分,半圆O的直径AB=100,在半圆弧上有一运动员C从B点沿半圆周匀速运动到M(最高点),此时由于自行车故障原地停留了一段时间,修理好继续以相同的速度运动到A点停止.设运动时间为t,点B到直线OC的距离为d,则下列图象能大致刻画d与t之间的关系是( )| A. | 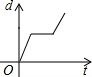 | B. | 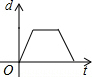 | C. | 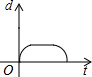 | D. | 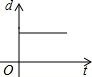 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
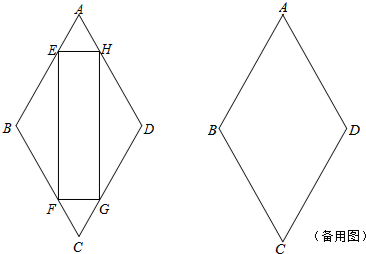
 如图,在?ABCD中,对角线AC、BD相交于点O,点E、F是AD上的点,且AE=EF=FD.连接BE、BF,使它们分别与AO相交于点G、H.
如图,在?ABCD中,对角线AC、BD相交于点O,点E、F是AD上的点,且AE=EF=FD.连接BE、BF,使它们分别与AO相交于点G、H.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x≥$\frac{1}{2}$ | B. | x≤1 | C. | $\frac{1}{2}$≤x≤1 | D. | 以上答案都不对 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com