
分析 首先根据勾股定理,得斜边是13cm,再根据其外接圆的半径是斜边的一半,得出其外接圆的半径.再利用直角三角形的内切圆半径等于两直角边的和与斜边之差的一半,计算出内切圆的半径,再作差计算即可.
解答 解:∵直角边长分别为5和12,
∴斜边=$\sqrt{{5}^{2}+{12}^{2}}$=13,
∴这个直角三角形的外接圆的半径为6.5.
∵直角三角形内切圆的半径等于两条直角边的和与斜边的差的一半,
∴其内切圆的半径是$\frac{12+5-13}{2}$=2,
∴6.5-2=4.5.
故答案为:4.5.
点评 本题考查的是三角形的内切圆与内心,熟知直角三角形的外接圆的半径是其斜边的一半;内切圆半径等于两直角边的和与斜边之差的一半这个结论是解题的关键.


 天天向上口算本系列答案
天天向上口算本系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
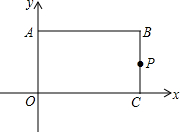 如图,矩形ABCO的两边AO=3,AB=4,以顶点O为原点,OC、OA所在直线分别为x轴、y轴建立如图所示平面直角坐标系,P是线段BC上一动点,设PC=m,已知点D在第一象限,且位于直线y=x+3上,若△APD是等腰直角三角形,则点D的坐标为(2,5)或(4,7).
如图,矩形ABCO的两边AO=3,AB=4,以顶点O为原点,OC、OA所在直线分别为x轴、y轴建立如图所示平面直角坐标系,P是线段BC上一动点,设PC=m,已知点D在第一象限,且位于直线y=x+3上,若△APD是等腰直角三角形,则点D的坐标为(2,5)或(4,7).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
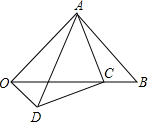 如图,△AOB是等腰直角三角形,AO=AB,∠OAB=90°,C为OB上任意一点,以AC为直角边作等腰直角三角形ACD,∠ACD=90°.连接OD,求∠AOD的度数.
如图,△AOB是等腰直角三角形,AO=AB,∠OAB=90°,C为OB上任意一点,以AC为直角边作等腰直角三角形ACD,∠ACD=90°.连接OD,求∠AOD的度数.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com