
【题目】如图1,在正方形ABCD中,点P为AD延长线上一点,连接AC、CP,过点C作CF⊥CP交于C,交AB于点F,过点B作BM⊥CF于点N,交AC于点M.
(1)若AP=![]() AC,BC=4,求S△ACP;
AC,BC=4,求S△ACP;
(2)若CP﹣BM=2FN,求证:BC=MC;
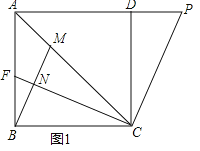
【答案】(1)S△ACP=7![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】试题分析:(1)由正方形的性质得出AB=BC=CD=4,∠ADC=∠CDP=∠ABC=∠BCD=90°,由勾股定理求出AC,得出AP,即可求出S△ACP;(2)在CF上截取NG=FN,连接BG,则CF-CG=2FN,证出∠BCF=∠DCP,由ASA证明△BCF≌△DCP,得出CF=CP,证出CG=BM,由SAS证明△ABM≌△BCG,得出∠AMB=∠BGC,因此∠BMC=∠BGF,由线段垂直平分线的性质得出BF=BG,得出∠BFG=∠BGF,因此∠BMC=∠CBM,即可得出结论
试题解析:(1)∵四边形ABC是正方形,
∴AD∥BC,AB=BC=CD=4,∠ADC=∠CDP=∠ABC=∠BCD=90°,
∴AC=![]() ,
,
∴AP=![]() AC=
AC=![]() ×
×![]() =
=![]() ,
,
∴S△ACP=![]() AP×CD=
AP×CD=![]() ×
×![]() ×4=7
×4=7![]() ;
;
(2)证明:在CF上截取NG=FN,连接BG,如图1所示:
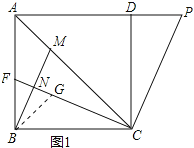
则CF﹣CG=2FN,
∵CF⊥CP,
∴∠PCF=90°,
∴∠BCF=∠DCP,
在△BCF和△DCP中, 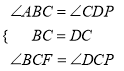 ,
,
∴△BCF≌△DCP(ASA),
∴CF=CP,
∵CP﹣BM=2FN,
∴CG=BM,
∵∠ABC=90°,BM⊥CF,
∴∠ABM=∠BCG,∠BFG=∠CBM,
在△ABM和△BCG中, 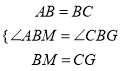 ,
,
∴△ABM≌△BCG(SAS),
∴∠AMB=∠BGC,
∴∠BMC=∠BGF,
∵GN=FN,BM⊥CF,
∴BF=BG,
∴∠BFG=∠BGF,
∴∠BMC=∠CBM,
∴BC=MC.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
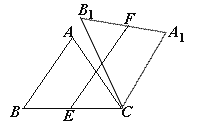
【题目】在△ABC中,AB=AC=5,cos∠ABC=![]() ,将△ABC绕点C顺时针旋转,得到△A1B1C.
,将△ABC绕点C顺时针旋转,得到△A1B1C.
(1)如图①,当点B1在线段BA延长线上时.①求证:BB1∥CA1;②求△AB1C的面积;
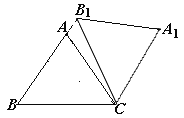
(2)如图②,点E是BC边的中点,点F为线段AB上的动点,在△ABC绕点C顺时针旋转过程中,点F的对应点是F1,求线段EF1长度的最大值与最小值的差.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列方程中变形正确的是( )
①3x+6=0变形为x+2=0;
②2x+8=5-3x变形为x=3;
③![]() +
+![]() =4去分母,得3x+2x=24;
=4去分母,得3x+2x=24;
④(x+2)-2(x-1)=0去括号,得x+2-2x-2=0.
A. ①③ B. ①②③ C. ①④ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李先生在2015年11月第2周星期五股市收盘时,以每股9元的价格买进某公司的股票1000股,在11月第3周的星期一至星期五,该股票每天收盘时每股的涨跌(单位:元)情况如下表:

注:表中记录的数据为每天收盘价格与前一天收盘价格的变化量,星期一的数据是与上星期五收盘价格的变化量.
(1)请你判断在11月的第3周内,该股票价格收盘时,价格最高的是哪一天?
(2)在11月第3周内,求李先生购买的股票每股每天平均的收盘价格.(结果精确到百分位)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】心理学家研究发现,一般情况下,一节课40分钟中,学生的注意力随教师讲课的变化而变化,开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数y随时间x(分钟)的变化规律如图所示(其中AB、BC分别为线段,CD为双曲线的一部分):
(1)开始上课后第五分钟时与第三十分钟时相比较,何时学生的注意力更集中?
(2)一道数学竞赛题,需要讲16分钟,为了效果较好,要求学生的注意力指标数最低达到36,那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com