
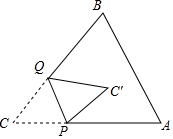
 如图,△ABC,∠C=45°,点P、Q分别在射线CA、CB上,且CP=2,将△ABC沿PQ折叠,点C落在平面上点C′处.
如图,△ABC,∠C=45°,点P、Q分别在射线CA、CB上,且CP=2,将△ABC沿PQ折叠,点C落在平面上点C′处.分析 (1)由PC′∥BC,推出∠CQP=∠QPC=∠CPQ,可得CP=CQ=2;
(2)由PC′⊥AC,∠C=45°,可知△CPC′是等腰直角三角形,由此即可解决问题;
(3)当折叠后重叠部分为等腰三角形时,符合条件的点Q共有5个;点C′在∠ACB的内部或一边上时,由折叠的性质、三角形内角和定理以及解直角三角形即可求出CQ的长;点C′在∠ACB的外部时,同理求出CQ的长即可
解答 解:(1)如图1中,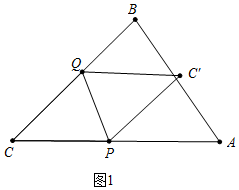
∵PC′∥BC,
∴∠CQP=∠QPC=∠CPQ,
∴CP=CQ=2.
(2)如图2中,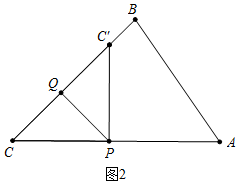
∵PC′⊥AC,∵∠C=45°,
∴△CPC′是等腰直角三角形,
∵∠QPC=∠QPC′,
∴CQ=QC′=$\frac{1}{2}$CC′=$\sqrt{2}$.
(3)①如图3中,当PQ=PM时,
∵∠PMQ=∠PQM=∠C+∠CPQ,
由折叠的性质得:∠CPQ=∠MPQ,
设∠CPQ=∠MPQ=x,
则∠PMQ=∠PQM=45°+x,
在△CPM中,由三角形内角和定理得:45°+x+x+45°+x=180°,
解得:x=30°,
∴∠CPQ=30°,
作QN⊥CP于N,设CN=a,
∵∠C=45°,
则QN=CN=a,CQ=$\sqrt{2}$a,PN=$\sqrt{3}$QN=$\sqrt{3}$a,
∵CN+PN=CP,
∴a+$\sqrt{3}$a=2,
解得:a=$\sqrt{3}$-1,
∴CQ=$\sqrt{2}$( $\sqrt{3}$-1)=$\sqrt{6}$-$\sqrt{2}$;
②如图4中,PQ=MQ,作QN⊥CA于N,
同①得:CQ=$\sqrt{6}$+$\sqrt{2}$;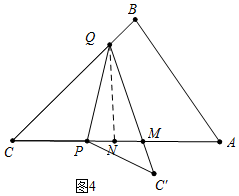
③如图5中,点C′在∠ACB的内部时,四边形CPC′Q是菱形,OQ=OP=2cm;
④如图6中,当点C′在BC边上时,△CPQ是等腰直角三角形,OQ=$\sqrt{2}$,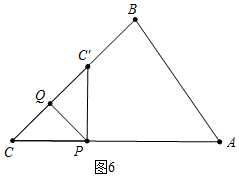
⑤如图7中,当点C′在AC的边上时,△CPQ是等腰直角三角形,CQ=2 $\sqrt{2}$;
综上所述,满足条件的CQ的值为($\sqrt{6}$-$\sqrt{2}$)cm或($\sqrt{6}$+$\sqrt{2}$)cm或2cm或$\sqrt{2}$cm或2$\sqrt{2}$cm.
点评 本题是三角形综合题目,考查了折叠的性质、等腰直角三角形的判定与性质、平行线的性质、等腰三角形的判定与性质、菱形的判定与性质、解直角三角形等知识;本题综合性强,有一定难度,熟练掌握折叠的性质,证明三角形是等腰直角三角形是解决问题的关键,注意分类讨论.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 年龄:(岁) | 13 | 14 | 15 | 16 |
| 人数 | 2 | 5 | 4 | 1 |
| A. | 众数是14 | B. | 极差是3 | C. | 中位数是14 | D. | 平均数是14.8 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com