
 如图,已知△ABC中,AB=$2\sqrt{5}$,AC=$4\sqrt{5}$,BC=6,点M为AB的中点,在线段AC上取点N,使△AMN与△ABC相似,求MN的长.
如图,已知△ABC中,AB=$2\sqrt{5}$,AC=$4\sqrt{5}$,BC=6,点M为AB的中点,在线段AC上取点N,使△AMN与△ABC相似,求MN的长. 分析 作MN∥BC交AC于点N,利用三角形的中位线定理可得MN的长;作∠ANM=∠B,利用相似可得MN的长.
解答 解:①图1,作MN∥BC交AC于点N,则△AMN∽△ABC,
有$\frac{AM}{AB}=\frac{MN}{BC}$,
∵M为AB中点,AB=$2\sqrt{5}$,
∴AM=$\sqrt{5}$,
∵BC=6,
∴MN=3;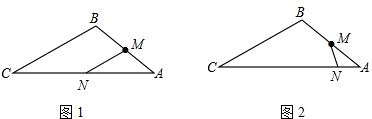
②图2,作∠ANM=∠B,则△ANM∽△ABC,
有$\frac{AM}{AC}=\frac{MN}{BC}$,
∵M为AB中点,AB=$2\sqrt{5}$,
∴AM=$\sqrt{5}$,
∵BC=6,AC=$4\sqrt{5}$,
∴MN=$\frac{3}{2}$,
∴MN的长为3或$\frac{3}{2}$.
点评 本题主要考查相似三角形的作图和相似三角形的判定以及存在性,解题的关键是注意相似作图及解答有多种情况.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,王大伯家屋后有一块长12m,宽8m的矩形空地,他在以长边BC为直径的半圆内种菜,他家养的一只羊平时拴在A处的一棵树上,为了不让羊吃到菜,拴羊的绳长可以选用( )
如图,王大伯家屋后有一块长12m,宽8m的矩形空地,他在以长边BC为直径的半圆内种菜,他家养的一只羊平时拴在A处的一棵树上,为了不让羊吃到菜,拴羊的绳长可以选用( )| A. | 9m | B. | 7m | C. | 5m | D. | 3m |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-1,-5) | B. | (5,-1) | C. | (5,-5) | D. | (-1,-1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com