
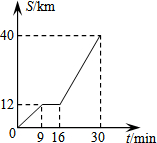
 如图是某汽车行驶的路程S(km)与时间t(min)的函数关系图.观察图中所提供的信息,解答下列问题:
如图是某汽车行驶的路程S(km)与时间t(min)的函数关系图.观察图中所提供的信息,解答下列问题:分析 (1)直接利用总路程÷总时间=平均速度,进而得出答案;
(2)利用路程不发生变化时,即可得出停留的时间;
(3)利用待定系数法求出S与t的函数关系式即可.
解答 解:(1)汽车在前9分钟内的平均速度是:$\frac{12}{9}$=$\frac{4}{3}$(km/min);
故答案为:$\frac{4}{3}$;
(2)汽车在中途停了:16-9=7(分钟);
故答案为:7;
(3)当16≤t≤30时,
则设S与t的函数关系式为:S=kt+b,
将(16,12),(30,40)代入得:
$\left\{\begin{array}{l}{16k+b=12}\\{30k+b=40}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=2}\\{b=-20}\end{array}\right.$,
故当16≤t≤30时,S与t的函数关系式为:S=2t-20.
点评 此题主要考查了一次函数的应用,利用数形结合得出点的坐标是解题关键.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:解答题
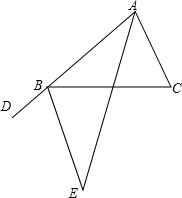 完成下面证明:如图,B是射线AD上一点,AE平分∠DAC,∠DAC=∠C=∠CBE
完成下面证明:如图,B是射线AD上一点,AE平分∠DAC,∠DAC=∠C=∠CBE查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在△ABC和△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,C、D、E三点在同一条直线上,连接BD、BE,以下三个结论:①BD=CE;②BD⊥CE;③∠ACE+∠DBC=45°,其中正确的是①②③(填序号)
如图,在△ABC和△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,C、D、E三点在同一条直线上,连接BD、BE,以下三个结论:①BD=CE;②BD⊥CE;③∠ACE+∠DBC=45°,其中正确的是①②③(填序号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
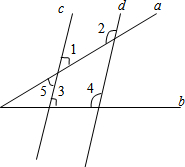 直线c、d分别被直线a、b所截,且∠3+∠4=180°,求证:∠2+∠5=180°.
直线c、d分别被直线a、b所截,且∠3+∠4=180°,求证:∠2+∠5=180°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{6}$ | B. | $\sqrt{\frac{1}{2}}$ | C. | $\sqrt{8}$ | D. | $\sqrt{27}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com