
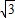 .PC是∠APB的平分线,∠BAC=30°.
.PC是∠APB的平分线,∠BAC=30°.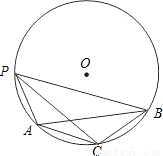
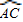 =
=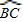 ,根据直径所对的圆周角是直角,根据特殊角的三角函数值求出PC的值,即可求出四边形PACB的面积.
,根据直径所对的圆周角是直角,根据特殊角的三角函数值求出PC的值,即可求出四边形PACB的面积.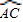 =
=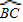 可知,AC=BC,又因为∠BAC=30°,所以∠ACB=120°,∠PAC与∠ACB互补,故BC∥AP且AC与PB不平行,四边形PACB是梯形.
可知,AC=BC,又因为∠BAC=30°,所以∠ACB=120°,∠PAC与∠ACB互补,故BC∥AP且AC与PB不平行,四边形PACB是梯形.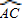 =
=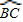 .(1分)
.(1分)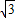 ,
,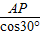 =
=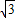 •
•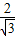 =2.(4分)
=2.(4分) PC•AB=
PC•AB= ×2×
×2×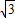
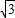 .(6分)
.(6分)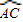 =
=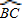 ,
,

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:2005年广西南宁市中考数学试卷(大纲卷)(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2005年广西南宁市中考数学试卷(大纲卷)(解析版) 题型:选择题
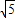 ,OC=2,则AC的长是( )
,OC=2,则AC的长是( )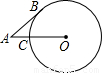
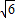 -1
-1
查看答案和解析>>
科目:初中数学 来源:2005年广西南宁市中考数学试卷(大纲卷)(解析版) 题型:选择题
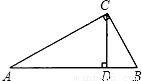




查看答案和解析>>
科目:初中数学 来源:2005年广西南宁市中考数学试卷(大纲卷)(解析版) 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com