
【题目】已知A(a,0),B(0,b),且a、b满足![]() .
.
(1)填空:a= ,b= ;
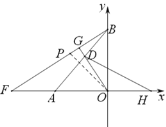
(2)如图1,将ΔAOB沿x轴翻折得ΔAOC,D为线段AB上一动点,OE⊥OD交AC于点E,求S四边形ODAE。
(3)如图2,D为AB上一点,过点B作BF⊥OD于点G,交x轴于点F,点H为x轴正半轴上一点,∠BFO=∠DHO,求证:AF=OH.

【答案】(1)a=-3,b=3;(2)4.5;(3)见解析.
【解析】
(1)根据二次根式的性质及绝对值的非负性可得:a+3=0,a+b=0,求出a、b即可;
(2)根据条件先证明△BOD≌△AOE,然后将四边形ODAE的面积转化为△AOB的面积进行计算即可;
(3)过点O作OP平分∠AOB交BF于P,先证明△BOP≌△OAD,推出OP=AD,再证明△PFO≌△DHA,利用全等的性质即可得出结论.
解:(1)∵a、b满足![]() ,
,
∴a+3=0,a+b=0,
∴a=-3,b=3;
(2)∵由(1)知:A(-3,0),B(0,3)
∴OA=OB=3
∵△AOB沿x轴翻折得△AOC
∴OA=OB=OC,∠AOB=∠AOC=90°
∴∠ABO=∠BAO=∠CAO=45°
又∵OE⊥OD,且∠BOD+∠AOD =∠AOB=90°
∴∠AOE+∠AOD=∠BOD+∠AOD=90°
∴∠AOE=∠BOD
∵∠DBO=∠EAO,OB=OA,∠BOD=∠AOE
∴△BOD≌△AOE(ASA)
∴S△AOE=S△BOD
∴S四边形ODAE=S△AOE + S△AOD = S△BOD + S△AOD =S△AOB=![]() ;
;
(3)过点O作OP平分∠AOB交BF于P,
∵OP平分∠AOB且OA=OB
∴∠AOP=∠BOP=45°
∴∠AOP=∠BOP=∠OAD
∵BG⊥OD
∴∠OBP+∠BOG=90°
又∵∠AOD+∠BOG=90°
∴∠OBP=∠AOD
∵OB=OA
∴△BOP≌△OAD(ASA)
∴OP=AD
又∵∠PFO=∠DHO,∠FOP=∠HAD=45°
∴△PFO≌△DHA(AAS)
∴OF=AH
∴OF-OA=AH-OA,即AF=OH.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BE、CE分别是∠ABC和∠ACB的平分线,过点E作DF∥BC交AB于D,交AC于F,若AB =5,AC =4,则△ADF周长为( ).

A.7B.8C.9D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
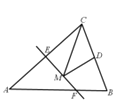
【题目】如图,等腰三角形ABC的底边BC长为6,面积是36,腰AC的垂直平分线EF分别交AC,AB边于E,F点.若点D为BC边的中点,点M为线段EF上一动点,则△CDM周长的最小值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,点
,点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上,连接
上,连接![]() ,
,![]() 、
、![]() 的平分线交于点
的平分线交于点![]() ,
,![]() 、
、![]() 的平分线交于点
的平分线交于点![]() .
.

![]() 求证:四边形
求证:四边形![]() 是矩形.
是矩形.
![]() 小明在完成
小明在完成![]() 的证明后继续进行了探索,过点
的证明后继续进行了探索,过点![]() 作
作![]() ,分别交
,分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,过点
,过点![]() 作
作![]() ,分别交
,分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,得到四边形
,得到四边形![]() .此时,他猜想四边形
.此时,他猜想四边形![]() 是菱形.请在下列框图中补全他的证明思路.
是菱形.请在下列框图中补全他的证明思路.
小明的证明思路:由![]() ,
,![]() ,
,![]() 易证,四边形
易证,四边形![]() 是平行四边形.要证□
是平行四边形.要证□![]() 是菱形,只要证
是菱形,只要证![]() .由已知条件________,
.由已知条件________,![]() ,可证
,可证![]() ,故只要证
,故只要证![]() ,即证
,即证![]() ,易证________,________,故只要证
,易证________,________,故只要证![]() ,易证
,易证![]() ,
,![]() ,________,故得
,________,故得![]() ,即可得证.
,即可得证.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,已知点A(-1,4),B(-2,2),C(1,1).

(1)作ΔABC关于x轴对称的△A1B1C1,并写出点A1,B1,C1的坐标,
(2)作△ABC关于y轴对称的△A2B2C2,并写出点A2,B2,C2的坐标,
(3)观察点A1,B1,C1和A2,B2,C2的坐标,请用文字语言归纳点A1和A2,B1和B2,C1和C2坐标之间的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,∠B=90°,AB=8cm,BC=6cm,点P从点A开始沿△ABC的边做逆时针运动,且速度为每秒1cm;点Q从点B开始沿△ABC的边做逆时针运动,且速度为每秒2cm,他们同时出发,设运动时间为t秒.
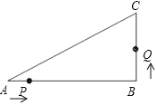
(1)出发2秒后,P,Q两点间的距离为多少cm?
(2)在运动过程中,△PQB能形成等腰三角形吗?若能,请求出几秒后第一次形成等腰三角形;若不能,则说明理由.
(3)出发几秒后,线段PQ第一次把△ABC的周长分成相等两部分?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com