
【题目】如图平面直角坐标系,已知二次函数![]() (m>0)的图象与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,顶点为点D.
(m>0)的图象与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,顶点为点D.
(1)点B的坐标为 ,点D的坐标为 ;(用含有m的代数式表示)
(2)连接CD,BC.
①若![]() ,求二次函数的表达式;
,求二次函数的表达式;
②若把ABC沿着直线BC翻折,点A恰好在直线CD上,求二次函数的表达式.
【答案】(1)![]() ,
,![]() ;(2)①
;(2)①![]() ;②
;②![]()
【解析】
(1)令![]() 解方程求出
解方程求出![]() 的值,结合点B的位置可得答案,由顶点的横坐标公式求得顶点横坐标,再代入解析式求解纵坐标即可.
的值,结合点B的位置可得答案,由顶点的横坐标公式求得顶点横坐标,再代入解析式求解纵坐标即可.
(2)①过点D作DH⊥AB,过点C作CG⊥DH,得到AB//CG,利用平行线的性质,锐角三角函数得![]() ,
,![]() 从而可求解函数解析式,
从而可求解函数解析式,
②过点B作BM⊥AC,BN⊥CD,由翻折得到角平分线,利用角平分线的性质得![]() ,利用三角形面积关系得到
,利用三角形面积关系得到![]() ,利用两点间距离公式列方程求解即可.
,利用两点间距离公式列方程求解即可.
解:(1)令![]()
![]()
![]()
![]()
![]() 点A在点B的左侧,
点A在点B的左侧,
![]()
![]()
![]() ,
,
![]() 抛物线的顶点横坐标为
抛物线的顶点横坐标为![]()
![]() 顶点纵坐标为:
顶点纵坐标为:![]()
![]() 顶点
顶点![]()
![]() .
.
故答案为: ![]() ,
,![]() .
.
(2)①过点D作DH⊥AB,过点C作CG⊥DH,
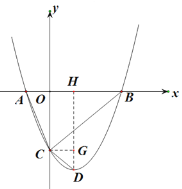
由题可知,C(0,﹣3m2),A(﹣m,0),B(3m,0),
∴![]() ,
,![]() ,
,
∵AB//CG
∴![]() ,
,
∴![]() ,
,
∵![]()
∴![]()
∴![]()
∴![]() ,
,
∴![]() ,
,
∴![]()
②过点B作BM⊥AC,BN⊥CD,
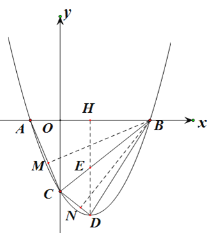
∵翻折
∴![]()
∵BM⊥AC,BN⊥CD,
∴![]()
由C(0,﹣3m2),A(﹣m,0),B(3m,0),D![]()
得![]() ,
,
![]()
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]()


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】在平行四边形ABCD中,对角线AC,BD交于点O,E是边AD上的一个动点(与点A,D不重合),连接EO并延长,交BC于点F,连接BE,DF.下列说法:
① 对于任意的点E,四边形BEDF都是平行四边形;
② 当∠ABC>90°时,至少存在一个点E,使得四边形BEDF是矩形;
③ 当AB<AD时,至少存在一个点E,使得是四边形BEDF是菱形;
④ 当∠ADB=45°时,至少存在一个点E,使得是四边形BEDF是正方形.
所有正确说法的序号是:_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形台球桌面ABCD上有两个球P,Q.PQ∥AB,球P连续撞击台球桌边AB,BC反射后,撞到球Q.已知点M,N是球在AB,BC边的撞击点,PQ=4,∠MPQ=30,且点P到AB边的距离为3,则四边形PMNQ的周长为__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点C是y轴正半轴上的一个动点,抛物线y=ax2-6ax+5a(a是常数,且a>0)过点C,与x轴交于点A、B,点A在点B的左边.连接AC,以AC为边作等边三角形ACD,点D与点O在直线AC两侧,连接BD,则BD的最小值是_________.
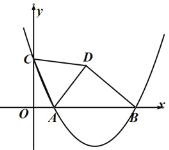
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线G:![]() 有最低点。
有最低点。
(1)求二次函数![]() 的最小值(用含m的式子表示);
的最小值(用含m的式子表示);
(2)将抛物线G向右平移m个单位得到抛物线G1。经过探究发现,随着m的变化,抛物线G1顶点的纵坐标y与横坐标x之间存在一个函数关系,求这个函数关系式,并写出自变量x的取值范围;
(3)记(2)所求的函数为H,抛物线G与函数H的图像交于点P,结合图像,求点P的纵坐标的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子中装有![]() 个小球,它们除了颜色不同外,其余都相同, 其中有 5 个白球,每次试验前,将盒子中的小球摇匀,随机摸出一个球记下颜色后再放回盒中.下表是摸球试验的一组统计数据:
个小球,它们除了颜色不同外,其余都相同, 其中有 5 个白球,每次试验前,将盒子中的小球摇匀,随机摸出一个球记下颜色后再放回盒中.下表是摸球试验的一组统计数据:
摸球次数( n ) | 50 | 100 | 150 | 200 | 250 | 300 | 500 |
摸到白球次( m ) | 28 | 60 | 78 | 104 | 123 | 152 | 251 |
白球频率( | 0.56 | 0.60 | 0.52 | 0.52 | 0.49 | 0.51 | 0.50 |
由上表可以推算出a大约是( )
A.10B.14C.16D.40
查看答案和解析>>
科目:初中数学 来源: 题型:
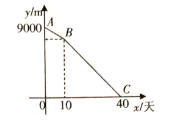
【题目】某街道需要铺设管线的总长为9000![]() ,计划由甲队施工,每天完成150
,计划由甲队施工,每天完成150![]() .工作一段时间后,因为天气原因,想要40天完工,所以增加了乙队.如图表示剩余管线的长度
.工作一段时间后,因为天气原因,想要40天完工,所以增加了乙队.如图表示剩余管线的长度![]() 与甲队工作时间
与甲队工作时间![]() (天)之间的函数关系图象.
(天)之间的函数关系图象.
(1)直接写出点![]() 的坐标;
的坐标;
(2)求线段![]() 所对应的函数解析式,并写出自变量
所对应的函数解析式,并写出自变量![]() 的取值范围;
的取值范围;
(3)直接写出乙队工作25天后剩余管线的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两所医院分别有一男一女共4名医护人员支援湖北武汉抗击疫情.
(1)若从甲、乙两医院支援的医护人员中分别随机选1名,则所选的2名医护人员性别相同的概率是 ;
(2)若从支援的4名医护人员中随机选2名,用列表或画树状图的方法求出这2名医护人员来自同一所医院的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com