
 △ADC,连接OD.
△ADC,连接OD. △ADC,
△ADC,
| 180°-(α-60°) |
| 2 |
| α |
| 2 |
| α |
| 2 |


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:
 21、如图,点D是等边三角形ABC内的一点,将△BDC绕点C顺时针旋转60°,试画出旋转后的三角形,并指出图中的全等图形以及它们的对应顶点、对应边和对应角.
21、如图,点D是等边三角形ABC内的一点,将△BDC绕点C顺时针旋转60°,试画出旋转后的三角形,并指出图中的全等图形以及它们的对应顶点、对应边和对应角.查看答案和解析>>
科目:初中数学 来源: 题型:
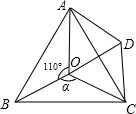
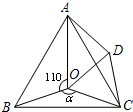 21、如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=a.以OC为一边作等边三角形OCD,连接AC、AD.
21、如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=a.以OC为一边作等边三角形OCD,连接AC、AD.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2011•清流县质检)星期天,小明在解答下列题目时卡壳了.
(2011•清流县质检)星期天,小明在解答下列题目时卡壳了.| 3 |
| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
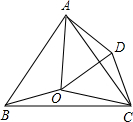 得到线段CD,连接OD、AD.
得到线段CD,连接OD、AD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com