(1)证明:延长AE交BC的延长线于点G. …
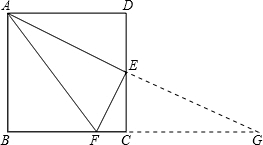
∵四边形ABCD是正方形,
∴AD∥CG,∠D=∠BCD=∠DCG,
∴∠DAE=∠G
∵∠FAE=∠EAD,
∴∠FAE=∠G
∴AF=FG …
∵E是DC的中点
∴DE=EC,
∵∠AED=∠GEC(对顶角相等)
∵∠D=∠ECG=90°,
∴△ADE≌△GCE (ASA)
∴AE=EG,
∴EF⊥AE. …
(2)解:若将(1)中的“正方形”改为“矩形”、“菱形”和“任意平行四边形”,其它条件不变,结论“EF⊥AE”仍然成立.
例如:“任意平行四边形”…
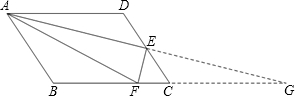
如图,延长AE交BC的延长线于G,
∵AD∥BC,E是DC的中点,
∴DE=CE,∠ADC=∠ECG,
∴∠DAE=∠G,
∴△ADE≌△GCE,
∴AE=EG,
同(1)一样可得△AFG是等腰三角形,
∴FE⊥AE.…
分析:(1)延长AE交BC的延长线于点G. 由四边形ABCD是正方形,则AD∥CG,从而得出∠DAE=∠G,再根据∠FAE=∠EAD,可得AF=FG,能证明△AEF≌△GEF,则AE=EG,
即EF⊥AE.
(2)例如:“任意平行四边形”,如图,延长AE交BC的延长线于G,由AD∥BC,及E是DC的中点,可得△ADE≌△GCE,得AE=EG,同(1)一样可得△AFG是等腰三角形,于是得FE⊥AE.
点评:本题考查了正方形的性质、全等三角形的判定和性质,是一道基础题,难度不大.

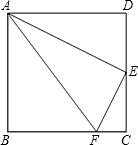 (1)如图,在正方形ABCD中,点E是CD的中点,点F是BC边上一点,且∠FAE=∠EAD,求证:EF⊥AE.
(1)如图,在正方形ABCD中,点E是CD的中点,点F是BC边上一点,且∠FAE=∠EAD,求证:EF⊥AE.



 中考解读考点精练系列答案
中考解读考点精练系列答案 如图,在正方形ABCD中,点E、F分别在边BC,CD上,如果AE=4,EF=3,AF=5,那么正方形ABCD的面积等于( )
如图,在正方形ABCD中,点E、F分别在边BC,CD上,如果AE=4,EF=3,AF=5,那么正方形ABCD的面积等于( ) (2012•温州三模)如图,在正方形ABCD中,点E、F、G、H均在其内部,且DE=EF=FG=GH=HB=2,∠E=∠F=∠G=∠H=60°,则正方形ABCD的边长AB=
(2012•温州三模)如图,在正方形ABCD中,点E、F、G、H均在其内部,且DE=EF=FG=GH=HB=2,∠E=∠F=∠G=∠H=60°,则正方形ABCD的边长AB= 如图,在正方形ABCD中,点E是AD的中点,连接BE、CE,点F是CE的中点,连接DF、BF,点M是BF上一点且
如图,在正方形ABCD中,点E是AD的中点,连接BE、CE,点F是CE的中点,连接DF、BF,点M是BF上一点且 如图,在正方形ABCD中,点M、N分别在AB、BC上,AB=4,AM=1,BN=0.75.
如图,在正方形ABCD中,点M、N分别在AB、BC上,AB=4,AM=1,BN=0.75.