
分析 (1)根据两种优惠方案分别求出需付费用,比较后即可得出结论;
(2)根据两种优惠方案需付费用相同,即可得出关于x的一元一次方程,解之即可得出结论.
解答 解:(1)方案a总费用20×250+(80-20)×40=7400(元),
方案b总费用20×250×90%+80×40×90%=7380(元).
∵7400>7380,
∴方案b付费较少.
(2)根据题意得:20×250+(x-20)×40=20×250×90%+40×90%x,
解得:x=75.
答:当x=75时,两种方案付费一样多.
点评 本题考查了一元一次方程的应用,解题的关键是:(1)根据两种优惠方案分别求出需付费用;(2)根据两种优惠方案需付费用相同,列出关于x的一元一次方程.


 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:解答题
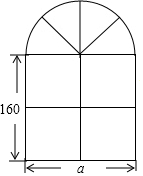 学习了整式的知识,请你解答下列实际问题:(图中长度单位:cm)窗户的形状如图所示,其上半部分是半圆形,下部是形状大小相同的四个小长方形.
学习了整式的知识,请你解答下列实际问题:(图中长度单位:cm)窗户的形状如图所示,其上半部分是半圆形,下部是形状大小相同的四个小长方形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
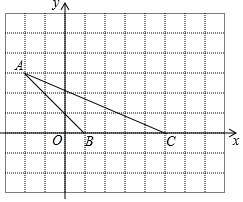 如图所示,小方格边长为1个单位,
如图所示,小方格边长为1个单位,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 了解本市中学生每天学习所用的时间,采用全面调查的方式 | |
| B. | 为保证运载火箭的成功发射,对其所有的零部件采用抽样调查的方式 | |
| C. | 了解某市每天的流动人口数,采用全面调查的方式 | |
| D. | 了解全市中学生的视力情况,采用抽样调查的方式 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
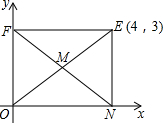 【阅读】
【阅读】查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
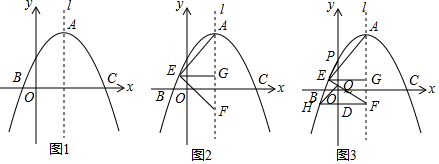
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com