
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 无法确定 |
分析 先得出每科的三名分值之和为:40÷5=8分,然后判断出单科三个名次的分值只有两种情况:单科第一名是5分,则:第二名为2,第三名为1分,和单科第一名为4分,则:第二名为3,第三名为1分,然后分情况讨论,找出符合题目的结论.
解答 解:∵甲得了22分,乙与丙各得了9分,总共22+9×2=40分,
∴每科的三名分值之和为:40÷5=8分,
∴单科三个名次的分值只有两种情况:单科第一名是5分,则:第二名为2,第三名为1分,和单科第一名为4分,则:第二名为3,第三名为1分,
①当第一名5分,第二名2分,第三名1分时,
∵乙在天文知识比赛中获得第一名,5分,余下4科,差9-5=4分,只能是四科全是第三名,4=1×4,
余下四个第一名,如果甲得3个第一名,得分3×5=15分,还余两科差:22-15=7分,此种情况不可能,
∴甲只能得四个第一名,得分;4×5=20分,还余1科,差2分,只能是第二名,
此时,余下一个第三名(天文),1分,余下四个第二名,得分2×4=8分,共9分,符合丙的得分,
此种情况甲得的第二名只能是天文,
∴其他的第二名全是丙,
∴获得互联网的第二名是丙;
②当第一名为4分,则:第二名为3,第三名为1分,
∵乙在天文知识比赛中获得第一名,得分4分,余下4科,差9-4=5分,只能是一个第二名,得2分,三个第三名,得分3,
余下四个第一名,如果甲得3个第一名,得分3×4=12分,还余两科差:22-12=10分,由于第一名才5分,所以甲只能得四个第一名,
∴甲得4个第一名,得分4×4=16分,还余两科差:22-16=6分,只能是两科第二名,2×3=6分,
此时,余下2科第二名,2×2=4分,3科第三名,3分,4+3=7分≠9分,不符合丙的得分,此种情况不可能,
即:只有第一名5分,第二名2分,第三名1分,这一种情况,获得互联网第二名的只有丙.
故选:C.
点评 此题是推理与论证,解本题的关键是结合题意认真审题,然后根据题意进行假设,通过分析推理,进而得出与题目相符的答案,得出结论.


科目:初中数学 来源: 题型:选择题
| A. | 向上、直线x=4、(4,5) | B. | 向上、直线x=-4、(-4,5) | ||
| C. | 向下、直线x=4、(4,5) | D. | 向下、直线x=-4、(-4,5) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
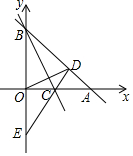 如图,在平面直角坐标系中,直线y=-x+2交x轴于点A,交y轴于点B,C是OA的中点,D为线段AB上一点,且∠ACD=∠BCO.
如图,在平面直角坐标系中,直线y=-x+2交x轴于点A,交y轴于点B,C是OA的中点,D为线段AB上一点,且∠ACD=∠BCO.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 若a•b>0,则a>0,b>0 | B. | 若a•b<0,则a<0,b>0 | ||
| C. | 若a•b=0,则a=0且b=0 | D. | 若a•b=0,则a=0或b=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 关于某直线成轴对称的两个图形一定能完全重合 | |
| B. | 线段是轴对称图形 | |
| C. | 全等的两个三角形一定关于某直线成轴对称 | |
| D. | 轴对称图形的对称轴至少有一条 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com