练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

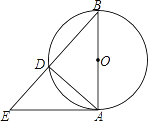
    【题目】如图，AB为⊙O的直径，AE为⊙O的切线，若tan∠ABE= ，AE=3，求BD的长．

    【答案】BD= ．

    【解析】

    由AB为⊙O的直径，得到∠ADB=90°，根据邻补角的定义得到∠ADE=90°，根据切线的性质得到∠EAB=90°，推出△EAD∽△EBA，根据相似三角形的性质得到，得到AE2=EDEB，根据三角函数的定义得到AB=6，由勾股定理得到BE=，即可得到结论．

    ∵AB为⊙O的直径， ∴∠ADB=90°，∴∠ADE=90°，

    ∵AE为⊙O的切线，

    ∴∠EAB=90°，

    ∵∠E=∠E，

    ∴△EAD∽△EBA，

    ∴，

    ∴AE2=EDEB，

    在Rt△AEB中，AE=3，tan∠ABE=，

    ∴，

    ∴AB=6，

    ∴BE=

    ∴32=ED3，

    ∴ED=，

    ∴BD=BE﹣ED=3﹣=．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

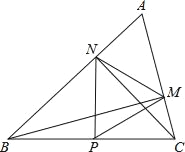
    【题目】如图，在△ABC中∠A=60°，BM⊥AC于点M，CN⊥AB于点N，P为BC边的中点，连接PM，PN，则下列结论：①PM=PN；②；③△PMN为等边三角形；④当∠ABC=45°时，BN=PC．其中正确的个数是（　　）

    A. 1个 B. 2个 C. 3个 D. 4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某学校20名数学教师的年龄（单位：岁）情况如下：29，42，58，37，53，52，49，24，37，46，42，55，40，38，50，26，54，26，44，52．

    (1)填写下面的频率分布表：

    分组

    频数

    频率

    19.5～29.5

    29.5～39.5

    39.5～49.5

    49.5～59.5

    合计

    (2)画出数据的频数分布直方图．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】几何体的三视图相互关联．已知直三棱柱的三视图如图，在△PMN中，∠MPN=90°，PN=4，sin∠PMN= ．

    （1）求BC及FG的长；

    （2）若主视图与左视图两矩形相似，求AB的长；

    （3）在（2）的情况下，求直三棱柱的表面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，折叠矩形ABCD，使点B落在对角线AC上的点F处，若BC＝8，AB＝6，则线段CE的长度是（　　）

    A. 3 B. 4 C. 5 D. 6

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知：AB是⊙O的直径，点C在⊙O上，CD是⊙O的切线，AD⊥CD于点D.E是AB延长线上一点，CE交⊙O于点F，连结OC，AC.

    (1)求证：AC平分∠DAO；

    (2)若∠DAO=105°，∠E=30°.①求∠OCE的度数.②若⊙O的半径为，求线段EF的长.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某景区商店以2元的批发价进了一批纪念品.经调查发现，每个定价3元，每天可以能卖出500件，而且定价每上涨0.1元，其销售量将减少10件.根据规定：纪念品售价不能超过批发价的2.5倍.

    （1）当每个纪念品定价为3.5元时，商店每天能卖出________件；

    （2）如果商店要实现每天800元的销售利润，那该如何定价？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小明参加某个智力竞答节目，答对最后两道单选题就顺利通关．第一道单选题有3个选项，第二道单选题有4个选项，这两道题小明都不会，不过小明还有一个“求助”没有用（使用“求助”可以让主持人去掉其中一题的一个错误选项）．

    （1）如果小明第一题不使用“求助”，那么小明答对第一道题的概率是　　．

    （2）如果小明将“求助”留在第二题使用，请用树状图或者列表来分析小明顺利通关的概率．

    （3）从概率的角度分析，你建议小明在第几题使用“求助”．（直接写出答案）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小明解方程=3出现了错误，解答过程如下：

    方程两边都乘以(x-2)，得1-(1-x)=3(第一步)

    去括号，得1-1+x=3(第二步)

    移项，合并同类项，得x=3(第三步)

    检验，当x=3时x-2≠0(第四步)

    所以x=3是原方程的解．(第五步)

    (1)小明解答过程是从第____步开始出错的，原方程化为第一步的根据是_____．

    (2)请写出此题正确的解答过程．

    查看答案和解析>>

    同步练习册答案