

分析 (1)根据喜欢A项目的有42人,所占的百分比是42%,即可求得调查的总人数,然后利用总人数减去其它组的人数即可求得喜欢B项目的人数,进而求得所占的百分比,补全统计图;
(2)利用总人数1500乘以对应的百分比即可;
(3)只要合理即可,答案不唯一.
解答 解:(1)调查的总人数是:42÷42%=100(人),
则B项目的人数是:100-42-8-20=30(人),
则B项目的人数所占的百分比是:$\frac{30}{100}$×100%=30%.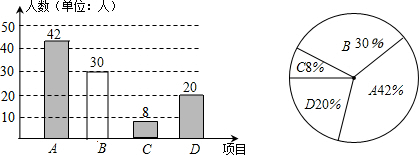 ;
;
(2)喜欢C类运动项目的学生人数:1500×8%=120(人);
(3)学生喜欢A项目的人数最多.
点评 本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:初中数学 来源: 题型:解答题
 如图为某风景区中古塔,大坝和湖的截面图,大坝顶端CE和水面平行,点C为大坝顶端拐角处,大坝的坡比i=3:1(即CG:FG=3:1),当小明和同伴从大坝的点F处沿着截面所在方向开始划船,划行20米到达点A处时,他们以仰角45°观察远方,正好看到古塔顶端的点D,且点C在视线AD上,当他们从点A继续沿原方向划船40米,到达点B处时,观察点D的仰角正好为30°.
如图为某风景区中古塔,大坝和湖的截面图,大坝顶端CE和水面平行,点C为大坝顶端拐角处,大坝的坡比i=3:1(即CG:FG=3:1),当小明和同伴从大坝的点F处沿着截面所在方向开始划船,划行20米到达点A处时,他们以仰角45°观察远方,正好看到古塔顶端的点D,且点C在视线AD上,当他们从点A继续沿原方向划船40米,到达点B处时,观察点D的仰角正好为30°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC,∠A=36°,∠B=72°,AC的垂直平分线分别交AC、AB于点D,E,则图中等腰三角形的个数为( )
如图,在△ABC,∠A=36°,∠B=72°,AC的垂直平分线分别交AC、AB于点D,E,则图中等腰三角形的个数为( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 直线CB:y=3x+b分别与x,y轴交于C(-2,0),B两点,过点B的直线交x轴正半轴于点A,且OB=OA.
直线CB:y=3x+b分别与x,y轴交于C(-2,0),B两点,过点B的直线交x轴正半轴于点A,且OB=OA.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x2-2x-3=x(x-2)-3 | B. | x2-2x-3=(x-1)2-4 | C. | (x+1)(x-3)=x2-2x-3 | D. | x2-2x-3=(x+1)(x-3) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 时 间 | 周一 | 周二 | 周三 | 周四 | 周五 | 周六 | 周日 |
| 最低气温(℃) | 5 | 7 | 2 | 6 | 2 | 2 | 4 |
| A. | 2,4.5,4 | B. | 2,3,4 | C. | 2,5,3 | D. | 2,4,4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com