
����Ŀ�����壺��ƽ��ֱ������ϵ�У�ͼ��G�ϵ�P��x��y����������y���������x�IJ�y��x��Ϊ��P���������������ͼ��G�����е������������е����ֵ��Ϊͼ��G��������ֵ����
��1�����A��2��1���������������������y����x2+3x+4��������ֵ����
��2��ij���κ�������x2+bx+c��c��0����������ֵ��Ϊ��1����B���C�ֱ��Ǵ˶��κ�����ͼ����x���y��Ľ��㣬�ҵ�B���C�������������ȣ���˶��κ����Ľ���ʽ��
��3����ͼ��ʾ�����κ���y����x2+px+q��ͼ�������������Ϊ2��һ�κ�����ͼ���ϣ��ı���DEFO�Ǿ��Σ���E������Ϊ��7��3������OΪ����ԭ�㣬��D��x���ϣ������κ���y����x2+px+q��ͼ������εı����ĸ�����ʱ����p��ȡֵ��Χ��
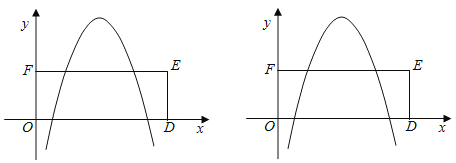
���𰸡�(1)-1,5;(2) y����x2+3x��2��(3) 2��p��10.
��������
��1��1-2=-1�������������Ϊ-1��y-x=-x2+3x+4-x=-��x-1��2+5����������ֵ��Ϊ5��
��2��������ã���C��0��c�����ʵ�B��C����ָ�������ȣ��ʵ�B��-c��0�����ѵ�B���������y=-x2+��1-c��x+c�ã�0=-��-c��2+b��-c��+c����ã�b=1-c���ʣ�y=-x2+��1-c��x+c���������ߵ�������ֵ��Ϊ-1��y-x=-x2+��1-c��x+c-x=-x2-cx+c����![]() =-1��������⣻
=-1��������⣻
��3�����������Ϊ2��һ�κ���Ϊ��y=x+2������ͼ1��ֱ������αߵĽ���Ϊ����1��3������Գ���Ϊ��-![]() =1����ã�p=2������ͼ2���ѵ�E��7��3������y=-��x-m��2+m+2����ã�m=5��10����ȥ10����������⣮
=1����ã�p=2������ͼ2���ѵ�E��7��3������y=-��x-m��2+m+2����ã�m=5��10����ȥ10����������⣮
�⣺��1��1��2����1�������������Ϊ��1��
y��x����x2+3x+4��x������x��1��2+5����������ֵ��Ϊ5��
��2��������ã���C��0��c�����ҵ�B��C�������������ȣ�
�ʵ�B����c��0�����ѵ�B���������y����x2+bx+c�ã�
0��������c��2+b����c��+c��
��ã�b��1��c��
�ʣ�y����x2+��1��c��x+c��
�������ߵ�������ֵ��Ϊ��1��
��y��x����x2+��1��c��x+c��x����x2��cx+c��
��![]() ����1��
����1��
��c����2��b��3��
�������ߵı���ʽΪ��y����x2+3x��2��
��3�����������Ϊ2��һ�κ���Ϊ��y��x+2��
��������y����x2+px+q��ͼ��Ķ�����y��x+2�ϣ�
���������ߵı���ʽΪ��y������x��m��2+m+2��
���������������3������ʱ����ͼ1��2��
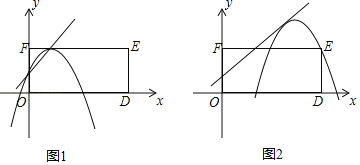
����ͼ1��ֱ������αߵĽ���Ϊ����1��3����
��Գ���Ϊ����![]() ��1����ã�p��2��
��1����ã�p��2��
����ͼ2���ѵ�E��7��3������y������x��m��2+m+2����ã�
m��5��10����ȥ10����
�ʩ�![]() ��5����ã�p��10��
��5����ã�p��10��
�ʶ��κ�����εı����ĸ�����ʱ����p��ȡֵ��Χ��2��p��10��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABC�ڽ���ԲO����BAC����ABC�Ľ�ƽ����AE��BE�ཻ�ڵ�E���ӳ�AE�����ԲO�ڵ�D������BD��DC������BCA=60��

��1������BED�Ĵ�С��
��2��֤������BEDΪ�ȱ������Σ�
��3������ADC=30����ԲO�İ뾶Ϊr����ȱ�������BED�ı߳���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
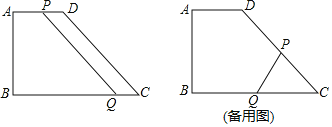
����Ŀ����ͼ����ֱ������ABCD�У���B��90����AD��BC����AD��4cm��AB��6cm��DC��10cm.������P��A���������ÿ��4cm���ٶ����߶�AD��DC��C���˶�������Q��C�������ÿ��5cm���ٶ���CB��B���˶�����Q�㵽��B��ʱ������P��Qͬʱֹͣ�˶�.���P��Qͬʱ���������˶���t�룬
(1)ֱ������ABCD��BCΪ_____cm���ܳ�Ϊ______cm.
(2)��tΪ����ʱ���ı���PQCD��Ϊƽ���ı��Σ�
(3)�Ƿ����t��ʹ��P�����߶�DC����PQ��DC�������ڣ������ʱt��ֵ���������ڣ�˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��D�ڡ�O��ֱ��AB�ӳ����ϣ���C�ڡ�O�ϣ�����D��ED��AD����AC���ӳ����ཻ�ڵ�E����CD��DE��
��1����֤��CDΪ��O�����ߣ�
��2����AB��8����BC��CEʱ����BD�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y��ax2+bx+c��ͼ����0��3��������1��0������3��0�����㣮
��1������κ�������ʽ��
��2����˵��y��x�ı仯�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
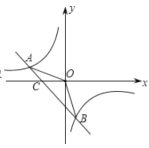
����Ŀ����ͼ����֪![]() ��
��![]() ��һ�κ���
��һ�κ���![]() �ͷ���������
�ͷ���������![]() ��ͼ����������㣮
��ͼ����������㣮
��1������������һ�κ����Ľ���ʽ��
��2����![]() �������
�������
��3������ͼ��ֱ��д��![]() ��
��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ���ı���![]() �У�
��![]() ��
��![]() ���ӳ�����һ�㣬
���ӳ�����һ�㣬![]() ��
��![]() ���ڵ�
���ڵ�![]() ��
��![]() ��
��
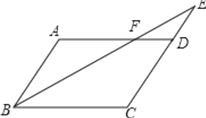
��1����֤��![]() ;
;
��2����![]() �����Ϊ4����ƽ���ı���
�����Ϊ4����ƽ���ı���![]() �������
�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�⣺��ͼ��1����2����ʾ�������У���������![]() �ύ��
�ύ��![]() ��
��![]() ����
����![]() �ύ��
�ύ��![]() ����
����![]() �������ߵĶ��㣬��
�������ߵĶ��㣬��![]() ƽ����
ƽ����![]() ���ֱ�������ĶԳ��ᣬ��
���ֱ�������ĶԳ��ᣬ��![]() �ڶԳ������˶��������̶ȵ�ֱ���ߵķ�������Ҫ�����������ͼ��
�ڶԳ������˶��������̶ȵ�ֱ���ߵķ�������Ҫ�����������ͼ��

��1����ͼ����������![]() ��ʹ�߶�
��ʹ�߶�![]() ��С��
����
��2����ͼ����������![]() ��ʹ�߶�
��ʹ�߶�![]() ���.
���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڳ�����ABCD�У�AB=6��BC=10��AE=2������BE��CE���߶�CD����һ��H������EDH��ֱ��EH�۵����۵����D����EC�ϵĵ�D��������D��N��AD�ڵ�N����EH���ڵ�M����١�D��MH���CBE���ǵ��������Σ��ڡ�BEHΪֱ�ǣ���DH����Ϊ![]() ����
����![]() ������˵����ȷ�ĸ�����( )
������˵����ȷ�ĸ�����( )
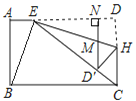
A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com