
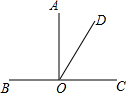
 如图,AO⊥BC,垂足为O,且∠COD-∠AOD=34°28′.求∠BOD的度数.
如图,AO⊥BC,垂足为O,且∠COD-∠AOD=34°28′.求∠BOD的度数.  阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
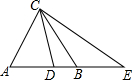 如图,△ABC中,AB=AC=8,D在AB上,E在AB的延长线上,∠ECB=∠DCB,AE=12.
如图,△ABC中,AB=AC=8,D在AB上,E在AB的延长线上,∠ECB=∠DCB,AE=12.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AD=2,CD=4.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AD=2,CD=4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
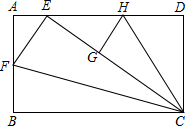 如图矩形ABCD是一张标准纸,长BC=AD=$\sqrt{2}$,AB=CD=1,把△BCF沿CF对折使点B恰好落在边AD上的点E处,再把△DCH沿CH对折使点D落在线段CE上的点G处.
如图矩形ABCD是一张标准纸,长BC=AD=$\sqrt{2}$,AB=CD=1,把△BCF沿CF对折使点B恰好落在边AD上的点E处,再把△DCH沿CH对折使点D落在线段CE上的点G处.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
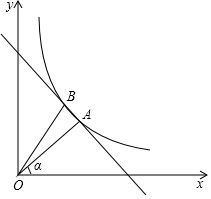 如图,在坐标系中,线段OA在第一象限,OA=5,OA与x轴的夹角α的正切tanα=$\frac{3}{4}$,反比例函数y=$\frac{k}{x}$(k≠0,x>0)图象经过点A,OA绕点O旋转后落在反比例函数y=$\frac{k}{x}$(x>0)的图象上另一点B,点B与x轴距离是4.
如图,在坐标系中,线段OA在第一象限,OA=5,OA与x轴的夹角α的正切tanα=$\frac{3}{4}$,反比例函数y=$\frac{k}{x}$(k≠0,x>0)图象经过点A,OA绕点O旋转后落在反比例函数y=$\frac{k}{x}$(x>0)的图象上另一点B,点B与x轴距离是4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点A,B,C都在格点上,请按要求回答问题或画图:
如图,点A,B,C都在格点上,请按要求回答问题或画图:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
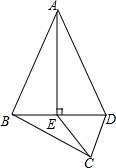 如图,四边形ABCD中,AB=AD,AE⊥BD于点E,连接CE.如果AB=13,BC=2$\sqrt{21}$,CD=4,AE=12,那么CE的长度是( )
如图,四边形ABCD中,AB=AD,AE⊥BD于点E,连接CE.如果AB=13,BC=2$\sqrt{21}$,CD=4,AE=12,那么CE的长度是( )| A. | 5 | B. | 8 | C. | 10 | D. | 无法计算 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com