练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在△ABC中，∠BAC＝110°，点E、G分别是AB、AC的中点，DE⊥AB交BC于D，FG⊥AC交BC于F，连接AD、AF．试求∠DAF的度数．

    【答案】40°．

    【解析】

    先利用三角形内角和得∠B+∠C＝70°，然后根据垂直平分线和等腰三角形的性质得到∠BAD＝∠B、∠CAF＝∠C，最后再利用角的和差即可完成解答.

    在△ABC中，∵∠BAC＝110°，

    ∴∠B+∠C＝180°﹣110°＝70°，

    ∵E、G分别是AB、AC的中点，

    又∵DE⊥AB，FG⊥AC，

    ∴AD＝BD，AF＝CF，

    ∴∠BAD＝∠B，∠CAF＝∠C，

    ∴∠DAF＝∠BAC﹣（∠BAD+∠CAF）

    ＝∠BAC﹣（∠B+∠C）＝110°﹣70°＝40°．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知△ABC中，BC＝6，AB、AC的垂直平分线分别交边BC于点M、N，若MN＝2，则△AMN的周长是_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某企业加工一台大型机械设备润滑用油千克，用油的重复利用率为，按此计算，加工一台大型机械设备的实际耗油量为千克．通过技术革新后，不仅降低了润滑用油量，同时也提高了用油的重复利用率，并且发现润滑用油量每减少千克，用油量的重复利用率增加，这样加工一台大型机械设备的实际耗油量下降到千克，问技术革新后，加工一台大型机械设备润滑用油量是多少千克？用油的重复利用率是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点B，E，C，F在同一条直线上，AB=DF，AC=DE，BE=FC．

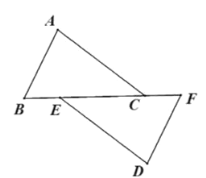
    （1）求证：AB∥DF；

    （2）当∠A=75°，∠DEF=38°时，求∠F的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，为中的一条射线，点在边上，于，交于点，交于点，于点，交于点，连接交于点．

    求证：四边形为矩形；

    若，试探究与的数量关系，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠ACB=90°，AC=3，AB=5．点P从点A出发，以每秒5个单位

    长度的速度沿AC方向运动，过点P作PQ⊥AB于点Q，当点Q和点B重合时，点P停止运动，以AP和AQ为边作APHQ．设点P的运动时间为t秒（t＞0）

    （1）线段PQ的长为　 　．（用含t的代数式表示）

    （2）当点H落在边BC上时，求t的值．

    （3）当APHQ与△ABC的重叠部分图形为四边形时，设四边形的面积为S，求S与t之间的函数关系式．

    （4）过点C作直线CD⊥AB于点D，当直线CD将APHQ分成两部分图形的面积比为1：7时，直接写出t的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在甲村至乙村间有一条公路，在C处需要爆破，已知点C与公路上的停靠站A的距离为300米，与公路上的另一停靠站B的距离为400米，且CA⊥CB，如图所示．为了安全起见，爆破点C周围半径250米范围内不得进入，问在进行爆破时，公路AB段是否有危险？请用你学过的知识加以解答.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】规定：四条边对应相等，四个角对应相等的两个四边形全等．某学习小组在研究后发现判定两个四边形全等需要五组对应条件，于是把五组条件进行分类研究，并且针对二条边和三个角对应相等类型进行研究提出以下几种可能：

    ①AB＝A1B1，AD＝A1D1，∠A＝∠A1，∠B＝∠B1，∠C＝∠C1；

    ②AB＝A1B1，AD＝A1D1，∠A＝∠A1，∠B＝∠B1，∠D＝∠D1；

    ③AB＝A1B1，AD＝A1D1，∠B＝∠B1，∠C＝∠C1，∠D＝∠D1；

    ④AB＝A1B1，CD＝C1D1，∠A＝∠A1，∠B＝∠B1，∠C＝∠C1．

    其中能判定四边形ABCD和四边形A1B1C1D1全等的有_____个．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图△ABC内接于⊙O，∠B=60°，CD是⊙O的直径，点P是CD延长线上一点，且AP=AC．

    （1）求证：PA是⊙O的切线；

    （2）若PD=，求⊙O的直径．

    查看答案和解析>>

    同步练习册答案