
����Ŀ����֪AB�ǡ�O���ң���P���Ż�AB�ϵ�һ�����㣬����AP������A��AP�Ĵ��ߣ���PB���ӳ����ڵ�C��
(1)��ͼ1��AC���O�ཻ�ڵ�D������D����O�����ߣ���PC�ڵ�E����DE��AB����֤��PA=PB��
(2)��ͼ2����֪��O�İ뾶Ϊ2��AB=2![]() ��
��
�ٵ���P���Ż�AB���˶�ʱ����C�Ķ���Ϊ�� ���㣻
�ڵ���P���Ż�AB���˶�ʱ����ABP�������֮�仯�����ABP��������ֵ��
�۵���P���Ż�AB���˶�ʱ����ABC�������֮�仯����ABC����������ֵΪ�� ����
���𰸡�(1)֤����������(2)��30����3![]() ����6+3
����6+3![]() ��
��
��������
��1������90���Բ�ܽ����Ե�����ֱ���ɵ�PD��ֱ�������DE��������DE��AB���ɵ�AB��PD�����ô���������֤��
��2����ֻҪ�����AOB�Ķ��������֪��APC�Ķ��������á�C�͡�APC����Ĺ�ϵ�ɵá�C����������������Է�����PD��ABʱ�������������á�C����ֵ�����֪��C��ABΪ�ҵ�ͬһ��Բ���˶��������ҵ�C���ںδ���ʹ�á�ABC���������Ӷ���ֵ��
��1����ͼ1������DP��AB�ڵ�F��
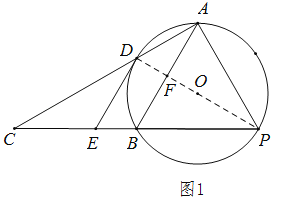
��CA��AP����DP����O��ֱ����
��DE����O����������DE��DP��
�֡�DE��AB����AB��DP����DP��ֱƽ��AB����������������PA��PB��
��2��������OA��OB���ɣ�1��֪��DP��ֱƽ��AB��
��AB��2![]() ����AF��BF
����AF��BF![]() ��
��
����O�İ뾶��2����OA��OB��2����sin��AOF![]() �����AOF��60�㣬���AOB��120�㣬���APB
�����AOF��60�㣬���AOB��120�㣬���APB![]() ��AOB��60�㣮
��AOB��60�㣮
��CA��AP�����C+��APB��90�㣬���C��30�㣻
������P���Ż�AB���˶�ʱ����ABP������ɵ�P��AB�ľ��������

����ͼ�ε����ʿ�֪����ͼ2������P�˶���PD��ABʱ��PF������������
��OA��2��PD��AB����AOF��60�㣬��OF��1����PF��OF+OP��1+2��3�����ABP��������ֵ����![]() ABPF
ABPF![]() 3��3
3��3![]() ��
��
������֪�ڱ仯�����С�ACB��30�����������C����ABΪ�ҵ�ij��Բ���˶��������Բ��Բ��ΪH����ͼ3��ʾ��
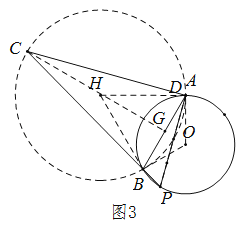
����AH��BH�����AHB��2��ACB��60�㣮
��AH��BH�����ABH�ǵȱ���������
��AB��2![]() ������H�İ뾶HA��2
������H�İ뾶HA��2![]() ����CG��AB����Ȼ����C���˶���CG����Բ��Hʱ��ABC��������
����CG��AB����Ȼ����C���˶���CG����Բ��Hʱ��ABC��������
��ʱ��CG��CH+HG��CH��2![]() ��
��
��HG��AB��AB��2![]() ����HG��AHsin60�㣽3����CG��2
����HG��AHsin60�㣽3����CG��2![]() 3�����ABC������ֵ����
3�����ABC������ֵ����
![]() ABCG
ABCG![]() ��2
��2![]() 3����6+3
3����6+3![]() ��
��


 ��1����Ԫ�¿�������ĩϵ�д�
��1����Ԫ�¿�������ĩϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η���x2+��2k+3��x+k2=0����������ȵ�ʵ����x1��x2��
��1����k��ȡֵ��Χ��
��2����![]() =��1����k��ֵ��
=��1����k��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
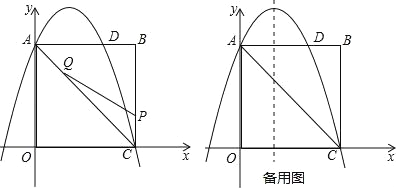
����Ŀ����ͼ���ھ���OABC�У���OΪԭ�㣬��A������Ϊ��0��8������C������Ϊ��6��0����������y����![]() x2+bx+c������A��C����AB���ڵ�D��
x2+bx+c������A��C����AB���ڵ�D��
��1���������ߵĺ�������ʽ��
��2����PΪ�߶�BC��һ�����㣨�����C�غϣ�����QΪ�߶�AC��һ�����㣬AQ��CP������PQ����CP��m����CPQ�����ΪS��
����S����m�ĺ�������ʽ��
�ڵ�S���ʱ����������y����![]() x2+bx+c�ĶԳ���l�ϣ������ڵ�F��ʹ��DFQΪֱ�������Σ���ֱ��д�����з��������ĵ�F�����ꣻ�������ڣ���˵�����ɣ�
x2+bx+c�ĶԳ���l�ϣ������ڵ�F��ʹ��DFQΪֱ�������Σ���ֱ��д�����з��������ĵ�F�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�̽�������������һ������A���Ƿ������һ������B�������ܳ�������ֱ�����֪�����ܳ��������һ�룿����������пո�
��1������֪����A�ı߳��ֱ�Ϊ6��1ʱ��С��ͬѧ�������о��ģ�
��������ε����߷ֱ���x��y��������÷����飺 ����ȥy����ã�2x2��7x+6=0��
����ȥy����ã�2x2��7x+6=0��
�ߡ�=49��48��0��
��x1=_____��x2=_______��
������Ҫ��ľ���B���ڣ�
��2�������֪����A�ı߳��ֱ�Ϊ2��1���������С���ķ����о��Ƿ��������Ҫ��ľ���B��
��3���������A�ı߳�Ϊm��n�������о�����ʲô����ʱ������B���ڣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����8��8�������е�ÿ��С�����α߳�����1���߶ν��������㣮����������Щ��㣬�ɵõ�һЩ�߶Σ���Ҫ����ͼ��
(1)�뻭����ABC�ĸ�AD��
(2)�����Ӹ�㣬��һ���߶ν�ͼ����ABC�ֳ������ȵ������֣�
(3)ֱ��д����ABC�������_____________.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�E��AD�ߵ��е㣬BE��AC������Ϊ��F������DF�����������ĸ����ۣ��١�AEF�ס�CAB����CF��2AF����DF��DC����tan��CAD��![]() ��������ȷ�Ľ�����( )
��������ȷ�Ľ�����( )

A. 4�� B. 3�� C. 2�� D. 1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��E�ǡ�AOB��ƽ������һ�㣬EC��OB��ED��OA��C��D�Ǵ��㣬����CD���ҽ�OE�ڵ�F.
��1����֤��OE��CD�Ĵ�ֱƽ����.
��2������AOB=60������̽��OE��EF֮����ʲô������ϵ����֤����Ľ��ۡ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ABC�У���ACB��90�㣬AC��BC��
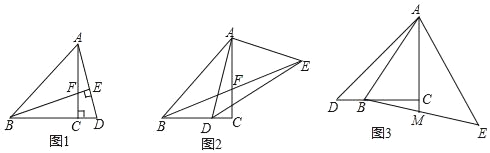
��1����ͼ1����D��BC���ӳ����ϣ���AD����B��BE��AD��E����AC�ڵ�F����֤��AD��BF��
��2����ͼ2����D���߶�BC�ϣ���AD����A��AE��AD����AE��AD����BE��AC��F����DE����BD��CF�к�������ϵ��������֤����
��3����ͼ3����D��CB�ӳ����ϣ�AE��AD��AE��AD������BE��AC���ӳ��߽�BE�ڵ�M����AC��3MC����ֱ��д��![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
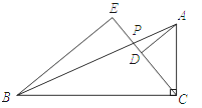
����Ŀ����֪����ͼ��Rt��ABC�У���ACB=90�㣬P�DZ�AB��һ�㣬AD��CP��BE��CP������ֱ�ΪD��E����֪AB=3![]() ��BC=3
��BC=3![]() ��BE=5����DE�ij���
��BE=5����DE�ij���
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com