
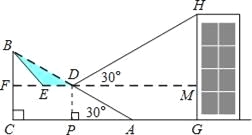
【题目】如图,已知斜坡AB长为80米,坡角(即∠BAC)为30°,BC⊥AC,现计划在斜坡中点D处挖去部分坡体(用阴影表示)修建一个平行于水平线CA的平台DE和一条新的斜坡BE.
(1)若修建的斜坡BE的坡角为45°,求平台DE的长;(结果保留根号)
(2)一座建筑物GH距离A处36米远(即AG为36米),小明在D处测得建筑物顶部H的仰角(即∠HDM)为30°.点B、C、A、G、H在同一个平面内,点C、A、G在同一条直线上,且HG⊥CG,求建筑物GH的高度.(结果保留根号)

【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)根据题意得出∠BEF=45°,解直角△BDF,求出BF,DF,进而得出EF的长,即可得出答案;
(2)利用在Rt△DPA中,DP=![]() AD,以及PA=ADcos30°进而得出DM的长,利用HM=DMtan30°得出即可.
AD,以及PA=ADcos30°进而得出DM的长,利用HM=DMtan30°得出即可.
试题解析:(1)∵修建的斜坡BE的坡角为45°,
∴∠BEF=45°,
∵∠DAC=∠BDF=30°,AD=BD=40,
∴BF=EF=![]() BD=20,DF=20
BD=20,DF=20![]() ,
,
∴DE=DF﹣EF=20![]() ﹣20,
﹣20,
∴平台DE的长为(20![]() ﹣20)米;
﹣20)米;
(2)过点D作DP⊥AC,垂足为P.
在Rt△DPA中,DP=![]() AD=
AD=![]() ×40=20,PA=ADcos30°=20
×40=20,PA=ADcos30°=20![]() ,
,
在矩形DPGM中,MG=DP=20,DM=PG=PA+AG=20![]() +36.
+36.
在Rt△DMH中,HM=DMtan30°=(20![]() +36)×
+36)×![]() =20+12
=20+12![]() ,
,
则GH=HM+MG=20+12![]() +20=40+12
+20=40+12![]() .
.
答:建筑物GH高为(40+12![]() )米.
)米.


科目:初中数学 来源: 题型:
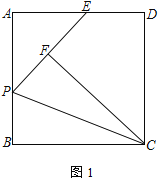
【题目】如图,正方形ABCD中,点P为AB边上一点,将△BCP沿CP翻折至△FCP位置,延长至PF交边AD于E点.
(1) 求证:EF=DE.
(2) 若DF延长线与CP延长线交于G点,求![]() 的值.
的值.
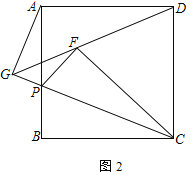
(3) 在(2)的条件下,若正方形的边长为![]() ,
, ![]() ,直接写出DG的长为___________.
,直接写出DG的长为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
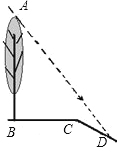
【题目】如图,坡面CD的坡比为![]() ,坡顶的平地BC上有一棵小树AB,当太阳光线与水平线夹角成60°时,测得小树的在坡顶平地上的树影BC是3米,斜坡上的树影CD是
,坡顶的平地BC上有一棵小树AB,当太阳光线与水平线夹角成60°时,测得小树的在坡顶平地上的树影BC是3米,斜坡上的树影CD是![]() 米,则小树AB的高是 米.
米,则小树AB的高是 米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】联合国规定每年的6月5日是“世界环境日”,为配合今年的“世界环境日”宣传活动,某校课外活动小组对全校师生开展了以“爱护环境,从我做起”为主题的问卷调查活动,将调查结果分析整理后,制成了上面的两个统计图.
其中:A:能将垃圾放到规定的地方,而且还会考虑垃圾的分类;
B:能将垃圾放到规定的地方,但不会考虑垃圾的分类;
C:偶尔会将垃圾放到规定的地方;
D:随手乱扔垃圾.
根据以上信息回答下列问题:
(1)该校课外活动小组共调查了多少人?并补全上面的条形统计图;
(2)如果该校共有师生2400人,那么随手乱扔垃圾的约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△ECD都是等腰直角三角形,∠ACB=∠DCE=∠90°,D为AB边上一点. 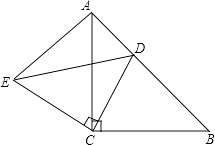
(1)求证:△ACE≌△BCD;
(2)若AD=6,BD=8,求ED的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两同学的家与学校的距离均为3000米.甲同学先步行600米,然后乘公交车去学校、乙同学骑自行车去学校.已知甲步行速度是乙骑自行车速度的![]() ,公交车的速度是乙骑自行车速度的2倍.甲乙两同学同时从家发去学校,结果甲同学比乙同学早到2分钟.
,公交车的速度是乙骑自行车速度的2倍.甲乙两同学同时从家发去学校,结果甲同学比乙同学早到2分钟.
(1)求乙骑自行车的速度;
(2)当甲到达学校时,乙同学离学校还有多远?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com