
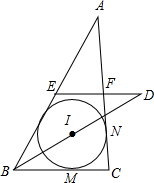
 如图,△ABC的内切圆I分别切BC、AC于点M、N,点E、F分别为边AB、AC的中点,D是直线EF与BI的交点.证明:M、N、D三点共线.
如图,△ABC的内切圆I分别切BC、AC于点M、N,点E、F分别为边AB、AC的中点,D是直线EF与BI的交点.证明:M、N、D三点共线. =
= ,
, ,
, DMB,
DMB, ∠ACB,
∠ACB, ∠ACB,
∠ACB, ∠ACB,
∠ACB, ∠ACB,
∠ACB, =
= ,变形得
,变形得 ,根据三角形相似的判定方法可得到△BAI∽△BDM,则∠AIB=DMB,又由于点I为△ABC的内心,根据内心的性质得∠AIB=90°+
,根据三角形相似的判定方法可得到△BAI∽△BDM,则∠AIB=DMB,又由于点I为△ABC的内心,根据内心的性质得∠AIB=90°+ ∠ACB,所以∠DMB=90°+
∠ACB,所以∠DMB=90°+ ∠ACB,而∠DMB=∠BMI+∠4=90°+∠4,所以∠4=
∠ACB,而∠DMB=∠BMI+∠4=90°+∠4,所以∠4= ∠ACB,易得∠4=∠5,根据四点共圆的判定方法得到I、M、C、G四点共圆,而∠IMC=90°,根据圆内接四边形的性质得∠IGC=90°,则IG⊥AC,而N为切点,所以N点与G点重合,于是得到M、N、D三点共线.
∠ACB,易得∠4=∠5,根据四点共圆的判定方法得到I、M、C、G四点共圆,而∠IMC=90°,根据圆内接四边形的性质得∠IGC=90°,则IG⊥AC,而N为切点,所以N点与G点重合,于是得到M、N、D三点共线.

 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案科目:初中数学 来源: 题型:
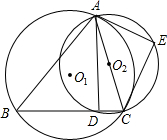 点E,连接AD、CE,若AC=7,AD=3
点E,连接AD、CE,若AC=7,AD=3| 5 |
| ||
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
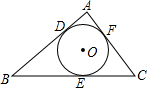 已知如图,△ABC内切⊙O于D、E、F三点,内切圆⊙O的半径为1,∠C=60°,AB=5,则△ABC的周长为( )
已知如图,△ABC内切⊙O于D、E、F三点,内切圆⊙O的半径为1,∠C=60°,AB=5,则△ABC的周长为( )| A、12 | ||
| B、14 | ||
C、10+2
| ||
D、10+
|
查看答案和解析>>
科目:初中数学 来源:解题升级 解题快速反应一典通 九年级级数学 题型:044
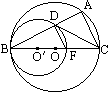
己知:如图,⊙O与![]() 内切于点B,BC是⊙O的直径,BC=6,BF为
内切于点B,BC是⊙O的直径,BC=6,BF为![]() 的直径,BF=4,⊙O的弦BA交
的直径,BF=4,⊙O的弦BA交![]() 于点D,连接DF、AC、CD.(1)求证:DF∥AC;(2)当∠ABC等于多少度时,CD与
于点D,连接DF、AC、CD.(1)求证:DF∥AC;(2)当∠ABC等于多少度时,CD与![]() 相切?并证明你的结论.(3)在(2)的前提下,连接FA交CD于点E,求AF、EF的长.
相切?并证明你的结论.(3)在(2)的前提下,连接FA交CD于点E,求AF、EF的长.
查看答案和解析>>
科目:初中数学 来源:同步题 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com