
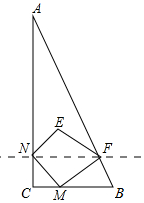
 如图,已知△ABC中,∠C=90°,点M从点C出发沿CB方向以1cm/s的速度匀速运动,到达点B停止运动,在点M的运动过程中,过点M作直线MN交AC于点N,且保持∠NMC=45°,再过点N作AC的垂线交AB于点F,连接MF.将△MNF关于直线NF对称后得到△ENF,已知AC=8cm,BC=4cm,设点M运动时间为t(s),△ENF与△ANF重叠部分的面积为y(cm2).
如图,已知△ABC中,∠C=90°,点M从点C出发沿CB方向以1cm/s的速度匀速运动,到达点B停止运动,在点M的运动过程中,过点M作直线MN交AC于点N,且保持∠NMC=45°,再过点N作AC的垂线交AB于点F,连接MF.将△MNF关于直线NF对称后得到△ENF,已知AC=8cm,BC=4cm,设点M运动时间为t(s),△ENF与△ANF重叠部分的面积为y(cm2).分析 (1)由已知得出CN=CM=t,FN∥BC,得出AN=8-t,由平行线证出△ANF∽△ACB,得出对应边成比例求出NF=$\frac{1}{2}$AN=$\frac{1}{2}$(8-t),由对称的性质得出∠ENF=∠MNF=∠NMC=45°,MN=NE,OE=OM=CN=t,由正方形的性质得出OE=ON=$\frac{1}{2}$FN,得出方程,解方程即可;
(2)分两种情况:①当0<t≤2时,由三角形面积得出y=-$\frac{1}{4}$t2+2t;
②当2<t≤4时,作GH⊥NF于H,由(1)得:NF=$\frac{1}{2}$(8-t),GH=NH,GH=2FH,得出GH=$\frac{2}{3}$NF=$\frac{1}{3}$(8-t),由三角形面积得出y=$\frac{1}{12}$(8-t)2(2<t≤4);
(3)当点E在AB边上时,y取最大值,连接EM,则EF=BF,EM=2CN=2CM=2t,EM=2BM,得出方程,解方程求出CN=CM=2,AN=6,得出BM=2,NF=$\frac{1}{2}$AN=3,因此EM=2BM=4,作FD⊥NE于D,由勾股定理求出EB=$\sqrt{E{M}^{2}+B{M}^{2}}$=2$\sqrt{5}$,求出EF=$\frac{1}{2}EB$=$\sqrt{5}$,由等腰直角三角形的性质和勾股定理得出DF=$\frac{\sqrt{2}}{2}$NF=$\frac{3\sqrt{2}}{2}$,在Rt△DEF中,由三角函数定义即可求出sin∠NEF的值.
解答 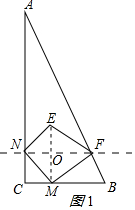 解:(1)能使得四边形MNEF为正方形;理由如下:
解:(1)能使得四边形MNEF为正方形;理由如下:
连接ME交NF于O,如图1所示:
∵∠C=90°,∠NMC=45°,NF⊥AC,
∴CN=CM=t,FN∥BC,
∴AN=8-t,△ANF∽△ACB,
∴$\frac{AN}{NF}=\frac{AC}{BC}$=$\frac{8}{4}$=2,
∴NF=$\frac{1}{2}$AN=$\frac{1}{2}$(8-t),
由对称的性质得:∠ENF=∠MNF=∠NMC=45°,MN=NE,OE=OM=CN=t,
∵四边形MNEF是正方形,
∴OE=ON=$\frac{1}{2}$FN,
∴t=$\frac{1}{2}$×$\frac{1}{2}$(8-t),
解得:t=$\frac{8}{5}$;
即在点M的运动过程中,能使得四边形MNEF为正方形,t的值为$\frac{8}{5}$;
(2)分两种情况:
①当0<t≤2时,y=$\frac{1}{2}$×$\frac{1}{2}$(8-t)×t=-$\frac{1}{4}$t2+2t,
即y=-$\frac{1}{4}$t2+2t(0<t≤2);
②当2<t≤4时,如图2所示:作GH⊥NF于H,
由(1)得:NF=$\frac{1}{2}$(8-t),GH=NH,GH=2FH,
∴GH=$\frac{2}{3}$NF=$\frac{1}{3}$(8-t),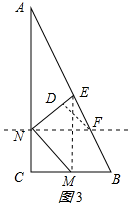
∴y=$\frac{1}{2}$NF′GH=$\frac{1}{2}$×$\frac{1}{2}$(8-t)×$\frac{1}{3}$(8-t)=$\frac{1}{12}$(8-t)2,
即y=$\frac{1}{12}$(8-t)2(2<t≤4);
(3)当点E在AB边上时,y取最大值,
连接EM,如图3所示:
则EF=BF,EM=2CN=2CM=2t,EM=2BM,
∵BM=4-t,
∴2t=2(4-t),
解得:t=2,
∴CN=CM=2,AN=6,
∴BM=4-2=2,NF=$\frac{1}{2}$AN=3,
∴EM=2BM=4,
作FD⊥NE于D,则EB=$\sqrt{E{M}^{2}+B{M}^{2}}$=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$,△DNF是等腰直角三角形,
∴EF=$\frac{1}{2}EB$=$\sqrt{5}$,DF=$\frac{\sqrt{2}}{2}$NF=$\frac{3\sqrt{2}}{2}$,
在Rt△DEF中,sin∠NEF=$\frac{DF}{EF}$=$\frac{\frac{3\sqrt{2}}{2}}{\sqrt{5}}$=$\frac{3\sqrt{10}}{10}$.
点评 本题是四边形综合题目,考查了正方形的判定与性质、相似三角形的判定与性质、勾股定理、三角函数、三角形面积的计算、等腰直角三角形的判定与性质等知识;本题综合性强,有一定难度.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 某商场新进一种商品,进货价为30元/件,按物价局规定,商品售价在30~70元之间,(包括30元和70元),经过一段销售发现,商品销量y(件/天)与售价x(元/件)之间满足一次函数关系,如图所示.
某商场新进一种商品,进货价为30元/件,按物价局规定,商品售价在30~70元之间,(包括30元和70元),经过一段销售发现,商品销量y(件/天)与售价x(元/件)之间满足一次函数关系,如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.5×10-8s | B. | 5×10-9s | C. | 5×10-8s | D. | 0.5×10-9s |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
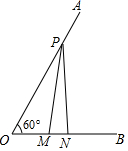 如图,已知∠AOB=60°,点P在边OA上,OP=10,点M、N在边OB上,PM=PN,若MN=2,则OM=( )
如图,已知∠AOB=60°,点P在边OA上,OP=10,点M、N在边OB上,PM=PN,若MN=2,则OM=( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 3 | C. | $-\frac{1}{4}$ | D. | $\frac{7}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com