
【题目】(1)自主阅读:在三角形的学习过程,我们知道三角形一边上的中线将三角形分成了两个面积相等三角形,原因是两个三角形的底边和底边上的高都相等,在此基础上我们可以继续研究:如图1,AD∥BC,连接AB,AC,BD,CD,则S△ABC=S△BCD.
证明:分别过点A和D,作AF⊥BC于F.DE⊥BC于E,由AD∥BC,可得AF=DE,又因为S△ABC=![]() ×BC×AF,S△BCD=
×BC×AF,S△BCD=![]() ×BC×DE .
×BC×DE .
所以S△ABC=S△BCD
由此我们可以得到以下的结论:像图1这样.
(2)问题解决:如图2,四边形ABCD中,AB∥DC,连接AC,过点B作BE∥AC,交DC延长线于点E,连接点A和DE的中点P,请你运用上面的结论证明:SABCD=S△APD
(3)应用拓展:
如图3,按此方式将大小不同的两个正方形放在一起,连接AF,CF,若大正方形的面积是80cm2,则图中阴影三角形的面积是 cm2.

【答案】(1)同底等高的两三角形面积相等;(2)证明见解析(3)40
【解析】试题分析:(1)利用图形直接得出:同底等高的两三角形面积相等(2)利用(1)的结论△ABC和△AEC的公共边AC上的高也相等,从而SABCD=S△APD。
(3)设正方形ABCD的边长为a,正方形DGFE的边长为b,阴影部分面积是S△AFG+S正方形DEFG+S△ADC﹣S△CEF,分别计算.
试题解析:
(1)利用图形直接得出:同底等高的两三角形面积相等;
故答案为:同底等高的两三角形面积相等.
(2)∵AB∥CE,BE∥AC,
∴四边形ABEC为平行四边形,
∴△ABC和△AEC的公共边AC上的高也相等,
∴S△ABC=S△AEC,
∴S梯形ABCD=S△ACD+S△ABC=S△ACD+S△AEC=S△AED.
(3)设正方形ABCD的边长为a,正方形DGFE的边长为b,
∵S△ACF=S四边形ACEF﹣S△CEF=S△AFG+S正方形DEFG+S△ADC﹣S△CEF=![]() ×b×(a﹣b)+b×b+
×b×(a﹣b)+b×b+![]() ×a×a﹣
×a×a﹣![]() ×b×(b+a)=
×b×(b+a)=![]() ab﹣
ab﹣![]() b2+b2+
b2+b2+![]() a2﹣
a2﹣![]() b2﹣
b2﹣![]() ab=
ab=![]() a2,
a2,
∴S△ACF=![]() S正方形ABCD=
S正方形ABCD=![]() ×80cm2=40cm2.
×80cm2=40cm2.
故答案为:40.


科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图象如图所示,有下列结论:①abc<0;②a+c>b;③3a+c<0;④a+b>m(am+b)(其中m≠1),其中正确的结论有______.
的图象如图所示,有下列结论:①abc<0;②a+c>b;③3a+c<0;④a+b>m(am+b)(其中m≠1),其中正确的结论有______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请你认真阅读材料,然后解答问题:
材料:在平面直角坐标系xOy中,对于任意三点A、B、C的“矩面积”,给出如下定义:“水平底”a:任意两点横坐标差的最大值,“铅垂高”h:任意两点纵坐标差的最大值,则“矩面积”![]() .
.
例如:三点的坐标分别为![]() ,
,![]() ,
,![]() ,则“水平底”
,则“水平底”![]() ,“铅垂高”
,“铅垂高”![]() ,“矩面积”
,“矩面积”![]() .
.
问题:
![]() 若
若![]() ,
,![]() ,
,![]() ,“水平底”
,“水平底”![]() ______,“铅垂高”
______,“铅垂高”![]() ______,“矩面积”
______,“矩面积”![]() ______.
______.
![]() 若
若![]() ,
,![]() ,
,![]() 的矩面积为12,求P点的坐标.
的矩面积为12,求P点的坐标.
![]() 若
若![]() ,
,![]() ,
,![]() ,请直接写出A、B、P三点的“矩面积”的最小值.
,请直接写出A、B、P三点的“矩面积”的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,反比例函数y=kx-1(x>0)的图象经过点A(1,2)和点B(m,n)(m>1),过点B作y轴的垂线,垂足为C.
(1)求该反比例函数解析式;
(2)当△ABC面积为2时,求点B的坐标.
(3)P为线段AB上一动点(P不与A、B重合),在(2)的情况下,直线y=ax﹣1与线段AB交于点P,直接写出a的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一小球从斜坡D点处抛出,球的抛出路线可以用二次函数)y=-x2+4x刻画,斜坡OA可以用一次函数y=![]() 刻画.
刻画.
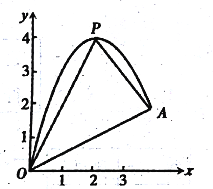
(1)请用配方法求二次函数图象的最高点P的坐标;
(2)小球的落点是A,求点A的坐标
(3)连接抛物线的最高点P与点O、A得△POA,求△POA的面积;
(4)在OA上方的抛物线上存在一点M(M与P不重合),△MOA的面积等于△POA的面积,请直接写出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() (a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
①4ac<b2;
②方程![]() 的两个根是x1=﹣1,x2=3;
的两个根是x1=﹣1,x2=3;
③3a+c>0
④当y>0时,x的取值范围是﹣1≤x<3
⑤当x<0时,y随x增大而增大
其中结论正确的个数是( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
某商店在2016年至2018年期间销售一种礼盒.2016年,该商店用2200元购进了这种礼盒并且全部售完:2018年,这种礼盒每盒的进价是2016年的一半,且该商店用2100元购进的礼盒数比2016年的礼盒数多100盒.那么,2016年这种礼盒每盒的进价是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
2014年,我国高速铁路营运里程已达1.6万千米;2015年,我国高速铁路营运里程已达1.9万千米;2016年,我国高速铁路营运里程已达2.2万千米;2017年,我囯高速铁路营运里程已达2.5万千米……截止到2017年底,我国高速铁路营运里程已稳居世界第一,分列世界第二至五名的国家为西班牙、德国、日本及法国.2017年底,五国高速铁路营运里程占全球高速铁路总营运里程的百分比如图所示.根据上述材料,解答下列问题

(1)请你用折线统计图表示2014-2017年我国高速铁路营运里程的发展情况;

(2)结合扇形统计图,解决问题:我国高速铁路营运里程占全球高速铁路总营运里程的百分比为: ;
(3)请你结合本题信息,预测中国高速铁路在2020年的运营状况,并写出你的一点感受和设想.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com