
下列说法中,正确的是( )
A. 若ac=bc,则a=b B. 若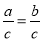 ,则a=b
,则a=b
C. 若a2=b2,则a=b D. 若|a|=|b|,则a=b
B 【解析】A选项中,根据等式的性质:“等式两边同时除以同一个不为0的数时,等式两边仍然相等”分析可知“若,则”是错误的,所以A中说法错误; B选项中,根据等式的性质:“等式两边同时乘以同一个数时,等式两边仍然相等”分析可知“若,则a=b”是正确的,所以B中说法正确; C选项中,因为“若,则或”,所以C中说法错误; D选项中,因为“若,则或”,所以D中说法错误; 故选...科目:初中数学 来源:2017-2018学年七年级数学北师大版上册:第3章 整式及其加减 单元测试卷 题型:解答题
用三角形和六边形按如图所示的规律拼图案.

(1)第4个图案中,三角形的个数有________个,六边形的个数有________个;
(2)第n(n为正整数)个图案中,三角形的个数与六边形的个数各有多少个?
(3)第2017个图案中,三角形的个数与六边形的个数各有多少个?
(4)是否存在某个符合上述规律的图案,其中有100个三角形与30个六边形?如果有,指出是第几个图案;如果没有,说明理由.
(1)10,4; (2)三角形的个数为 (2n+2)个,六边形的个数为n; (3)三角形的个数为4036个,六边形的个数为2017个; (4)不存在.理由见解析. 【解析】试题分析:观察图案可知:第一个图案有正三角形4个为2×2.第二图案比第一个图案多2个为2×2+2=6个,第三个图案比第二个多2个为2×3+2=8个,那么第n个就有正三角形(2n+2)个;第一个图案有一个正...查看答案和解析>>
科目:初中数学 来源:2017-2018学年七年级数学人教版上册:第4章 几何图形初步 单元测试卷 题型:单选题
生活中的实物可以抽象出各种各样的几何图形,如图所示蛋糕的形状类似于( )

A.圆柱体 B.球体 C.圆 D.圆锥体
A 【解析】 【解析】 蛋糕的形状类似于圆柱,故选:A.查看答案和解析>>
科目:初中数学 来源:2017-2018学年山东省德州市六校七年级(上)第一次联考数学试卷 题型:填空题
关于x的两个方程5x﹣3=4x与ax﹣12=0的解相同,则a= .
4 【解析】 试题分析:先求方程5x﹣3=4x的解,再代入ax﹣12=0,求得a的值. 【解析】 解方程5x﹣3=4x, 得x=3, 把x=3代入ax﹣12=0, 得3a﹣12=0, 解得a=4. 故填:4.查看答案和解析>>
科目:初中数学 来源:2017-2018学年山东省德州市六校七年级(上)第一次联考数学试卷 题型:单选题
下列解方程过程中,变形正确的是( )
A. 由2x?1=3得2x=3?1 B. 由 +1=
+1= +1.2得
+1.2得 +1=
+1= +12
+12
C. 由?75x=76得x=?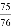 D. 由
D. 由 ?
? =1得2x?3x=6
=1得2x?3x=6
查看答案和解析>>
科目:初中数学 来源:云南省楚雄州2017-2018学年上学期期末教学质量监测九年级数学试卷 题型:解答题
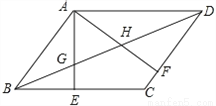
如图,在平行四边形ABCD中,AE⊥BC于E,AF⊥CD于F,BD与AE、AF交于G、H.
(1)求证:△ABE∽△ADF;
(2)若AG=AH,求证:四边形ABCD是菱形.
查看答案和解析>>
科目:初中数学 来源:云南省楚雄州2017-2018学年上学期期末教学质量监测九年级数学试卷 题型:单选题
如图,P(x,y)是反比例函数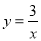 的图象在第一象限分支上的一个动点,PA⊥x轴于点A,PB⊥y轴于点B,随着自变量x的增大,矩形OAPB的面积( )
的图象在第一象限分支上的一个动点,PA⊥x轴于点A,PB⊥y轴于点B,随着自变量x的增大,矩形OAPB的面积( )

A. 增大 B. 减小 C. 不变 D. 无法确定
C 【解析】试题解析:依题意有矩形OAPB的面积=2×|k|=3,所以随着x的逐渐增大,矩形OAPB的面积将不变. 故选C.查看答案和解析>>
科目:初中数学 来源:陕西省2018届九年级上学期期中考试数学试卷 题型:解答题
(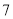 分)某超市对进货价为
分)某超市对进货价为 元/千克的某种苹果的销售情况进行统计,发现每天销售量
元/千克的某种苹果的销售情况进行统计,发现每天销售量 (千克)与销售价
(千克)与销售价 (元/千克)存在一次函数关系,如图.
(元/千克)存在一次函数关系,如图.

( )求
)求 关于
关于 的函数关系式.
的函数关系式.
( )应怎样确定销售价,使该品种苹果的每天销售利润最大?最大利润是多少?
)应怎样确定销售价,使该品种苹果的每天销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源:2017-2018学年黑龙江省哈尔滨市双城区七年级(上)期末数学试卷(五四学制) 题型:解答题
如图,已知线段AB和CD的公共部分为BD,且BD= AB=
AB= CD,线段AB、CD的中点E、F之间距离是20,求AB、CD的长.
CD,线段AB、CD的中点E、F之间距离是20,求AB、CD的长.
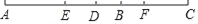
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com