
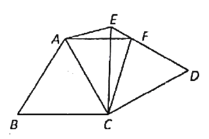
【题目】如图,将等边△ABC绕点C顺时针旋转90得到△DEC,∠ACD的平分线CF交DE于点F,连接AE,AF.
(1)求∠CEA度数;
(2)求证AF⊥CE.
【答案】(1)75°;(2)详见解析.
【解析】
(1)由等边△ABC绕点C顺时针旋转90![]() 得到△DEC,得到∠BCE=90
得到△DEC,得到∠BCE=90![]() ,∠ACB=60
,∠ACB=60![]() ,CE=AC,
,CE=AC,
求出∠ACE =30![]() ,再根据等边对等角及三角形的内角和即可得到答案;
,再根据等边对等角及三角形的内角和即可得到答案;
(2)根据CF平分∠ACD,利用SAS证明△ACF≌△DCF,得到∠CAF=∠D=60![]() ,再利用三角形内角和得到∠AHC =90
,再利用三角形内角和得到∠AHC =90![]() .
.
(1)∵等边△ABC绕点C顺时针旋转90![]() 得到△DEC,
得到△DEC,
∴∠BCE=90![]() ,∠ACB=60
,∠ACB=60![]() ,BC=CE=AC=CD,
,BC=CE=AC=CD,
∴∠ACE=∠BCE-∠ACB=30![]() ,
,
∵∠ACE+∠CEA+∠CAE=![]() ,∠CEA=∠CAE,
,∠CEA=∠CAE,
∴∠CEA= ![]()
(2)∵等边△ABC绕点C顺时针旋转90![]() 得到△DEC,
得到△DEC,
∴△DEC是等边三角形,
∴∠D=60![]() ,
,
∵CF平分∠ACD,
∴∠ACF=∠DCF,
又∵AC=CD,CF=CF,
∴△ACF≌△DCF,
∴∠CAF=∠D=60![]() ,
,
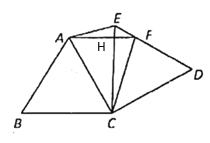
设AF交CE于H,
∵∠ACE =30![]() ,
,
∴∠AHC=![]() -∠ACE-∠CAF=90
-∠ACE-∠CAF=90![]() ,
,
∴AF⊥CE.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案科目:初中数学 来源: 题型:
【题目】不透明的口袋里装有红、黄、蓝三种颜色的小球若干个(小球除颜色外其余都相同),其中黄球2个,蓝球1个.若从中随机摸出一个球,摸到蓝球的概率是![]() .
.
(1)求口袋里红球的个数;
(2)第一次随机摸出一个球(不放回),第二次再随机摸出一个球,请用列表或画树状图的方法,求两次摸到的球恰是一黄一蓝的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
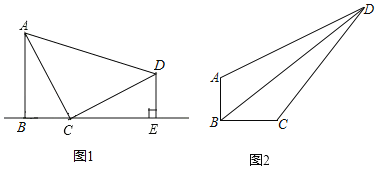
【题目】(1)如图1,已知AB⊥l,DE⊥l,垂足分别为B、E,且C是l上一点,∠ACD=90°,求证:△ABC∽△CED;
(2)如图2,在四边形ABCD中,已知∠ABC=90°,AB=3,BC=4,CD=10,DA=5![]() ,求BD的长.
,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为满足市场需求,某超市在八月十五“中秋节”来临前夕,购进一种品牌的月饼,每盒进价40元,根据以往的销售经验发现:当售价定为每盒45元时,每天可以卖出700盒,每盒售价每提高1元,每天要少卖出20盒.
![]() 写出每天的销售量
写出每天的销售量![]() 盒
盒![]() 与每盒月饼上涨
与每盒月饼上涨![]() 元
元![]() 之间的函数关系式.
之间的函数关系式.
![]() 当每盒售价定为多少元时,当天的销售利润
当每盒售价定为多少元时,当天的销售利润![]() 元
元![]() 最大?最大利润是多少?
最大?最大利润是多少?
![]() 为稳定物价,有关管理部门限定,这种月饼每盒的利润不得高于进价的
为稳定物价,有关管理部门限定,这种月饼每盒的利润不得高于进价的![]() ,那么超市每天获得最大利润是多少?
,那么超市每天获得最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线![]() 与y轴交于点A.
与y轴交于点A.
(1)直接写出点A的坐标;
(2)点A、B关于对称轴对称,求点B的坐标;
(3)已知点![]() ,
,![]() .若抛物线与线段PQ恰有两个公共点,结合函数图象,求a的取值范围.
.若抛物线与线段PQ恰有两个公共点,结合函数图象,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
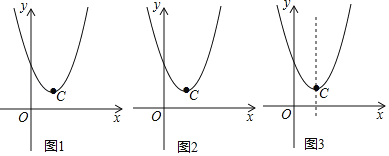
【题目】(1)抛物线y=ax2﹣2x+2经过点E(2,2),其顶点为C点.
①求抛物线的解析式,并直接写出C点坐标;
②将直线y=x沿y轴向上平移b(b>0)个单位长度交抛物线于A、B两点,若∠ACB=90°,求b的值.
(2)是否存在点D(1,m),使抛物线y=![]() x2﹣
x2﹣![]() x+
x+![]() 上任意一点P到x轴的距离等于P点到点D的距离,若存在,请求点D的坐标,若不存在,请说明理由.
上任意一点P到x轴的距离等于P点到点D的距离,若存在,请求点D的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=x2+mx交x轴的负半轴于点A.点B是y轴正半轴上一点,点A关于点B的对称点A′恰好落在抛物线上.过点A′作x轴的平行线交抛物线于另一点C.若点A′的横坐标为1,则A′C的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某养猪场对猪舍进行喷药消毒.在消毒的过程中,先经过![]() 的药物集中喷洒,再封闭猪舍
的药物集中喷洒,再封闭猪舍![]() ,然后再打开窗户进行通风.已知室内每立方米空气中含药量
,然后再打开窗户进行通风.已知室内每立方米空气中含药量![]() (
(![]() )与药物在空气中的持续时间
)与药物在空气中的持续时间![]() (
(![]() )之间的函数图象如图所示,其中在打开窗户通风前
)之间的函数图象如图所示,其中在打开窗户通风前![]() 与
与![]() 分别满足两个一次函数,在通风后
分别满足两个一次函数,在通风后![]() 与
与![]() 满足反比例函数.
满足反比例函数.
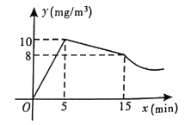
(1)求反比例函数的关系式;
(2)当猪舍内空气中含药量不低于![]() 且持续时间不少于
且持续时间不少于![]() ,才能有效杀死病毒,问此次消毒是否有效?
,才能有效杀死病毒,问此次消毒是否有效?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com