
学校美术作品展中,九年级8个班参展的作品(单位:件)分别为:3、5、2、4、3、2、3、4,则这组数据的中位数是( )
A.2 B.3 C.3.5 D.4
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2017届北京三十一中九年级上期中数学试卷(解析版) 题型:解答题
阅读下面材料:
如图1,在平面直角坐标系xOy中,直线y1=ax+b与双曲线y2= 交于A(1,3)和B(﹣3,﹣1)两点.
交于A(1,3)和B(﹣3,﹣1)两点.
观察图象可知:
①当x=﹣3或1时,y1=y2;
②当﹣3<x<0或x>1时,y1>y2,即通过观察函数的图象,可以得到不等式ax+b> 的解集.
的解集.
有这样一个问题:求不等式x3+4x2﹣x﹣4>0的解集.
某同学根据学习以上知识的经验,对求不等式x3+4x2﹣x﹣4>0的解集进行了探究.

下面是他的探究过程,请将(2)、(3)、(4)补充完整:
(1)将不等式按条件进行转化:
当x=0时,原不等式不成立;
当x>0时,原不等式可以转化为x2+4x﹣1> ;
;
当x<0时,原不等式可以转化为x2+4x﹣1< ;
;
(2)构造函数,画出图象
设y3=x2+4x﹣1,y4= ,在同一坐标系中分别画出这两个函数的图象.
,在同一坐标系中分别画出这两个函数的图象.
双曲线y4= 如图2所示,请在此坐标系中画出抛物线y3=x2+4x﹣1;(不用列表)
如图2所示,请在此坐标系中画出抛物线y3=x2+4x﹣1;(不用列表)
(3)确定两个函数图象公共点的横坐标
观察所画两个函数的图象,猜想并通过代入函数解析式验证可知:满足y3=y4的所有x的值为 ;
(4)借助图象,写出解集
结合(1)的讨论结果,观察两个函数的图象可知:不等式x3+4x2﹣x﹣4>0的解集为 .
查看答案和解析>>
科目:初中数学 来源:2016届浙江温州市龙湾区中考一模数学试卷(解析版) 题型:单选题
如下图,已知△ABC(AB<BC),用尺规在BC上确定一点P,使PA+PB=BC。则下面四种不同方法作图中准确的是( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:2016届福建泉州晋江市中考二模数学试卷(解析版) 题型:填空题
如图1,将半径为2的圆形纸片沿圆的两条互相垂直的直径AC、BD两次折叠后,得到如图2所示的扇形OAB,然后再沿OB的中垂线EF将扇形OAB剪成左右两部分,则∠OEF= °;右边部分经过两次展开并压平后所得的图形的周长为 .

查看答案和解析>>
科目:初中数学 来源:2016届福建泉州晋江市中考二模数学试卷(解析版) 题型:填空题
崖城13﹣1气田是我国海上最大合作气田,年产气约为3400000000立方米,将数据3400000000用科学记数法表示为 .
查看答案和解析>>
科目:初中数学 来源:2017届吉林长春德惠市九年级上期末数学试卷(解析版) 题型:解答题
如图,在平面直角坐标系xOy中,顶点为M的抛物线y=ax2+bx(a>0),经过点A和x轴正半轴上的点B,AO=OB=2,∠AOB=120°.
(1)求这条抛物线的表达式;
(2)连接OM,求∠AOM的大小;
(3)如果点C在x轴上,且△ABC与△AOM相似,求点C的坐标.

查看答案和解析>>
科目:初中数学 来源:2017届吉林长春德惠市九年级上期末数学试卷(解析版) 题型:解答题
如图,在∠ABC中,∠B=30°,AC= ,等腰直角△ACD斜边AD在AB边上,求BC的长.
,等腰直角△ACD斜边AD在AB边上,求BC的长.

查看答案和解析>>
科目:初中数学 来源:2017届湖北孝感安陆市九年级上期末数学试卷(解析版) 题型:解答题
请阅读下列材料,并完成相应的任务:
阿基米德折弦定理
阿基米德(archimedes,公元前287﹣公元前212年,古希腊)是有史以来最伟大的数学家之一,他与牛顿、高斯并成为三大数学王子.
阿拉伯Al﹣Binmi的译文中保存了阿基米德折弦定理的内容,苏联在1964年根据Al﹣Binmi译本出版了俄文版《阿基米德全集》,第一题就是阿基米德折弦定理.
阿基米德折弦定理:如图1,AB和BC是⊙O的两条弦(即折线ABC是圆的一条折弦),BC>AB,M是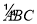 的中点,则从M向BC所作垂线的垂足D是折弦ABC的中点,即CD=AB+BD.下面是运用“截长法”证明CD=AB+BD的部分证明过程.证明:如图2,在CB上截取CG=AB,连接MA,MB,MC和MG.
的中点,则从M向BC所作垂线的垂足D是折弦ABC的中点,即CD=AB+BD.下面是运用“截长法”证明CD=AB+BD的部分证明过程.证明:如图2,在CB上截取CG=AB,连接MA,MB,MC和MG.
∵M是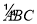 的中点,
的中点,
∴MA=MC.
…
任务:
(1)请按照上面的证明思路,写出该证明的剩余部分;
(2)填空:如图3,已知等边△ABC内接于⊙O,AB=2,D为 上一点,∠ABD=45°,AE⊥BD于点E,则△BDC的周长是 .
上一点,∠ABD=45°,AE⊥BD于点E,则△BDC的周长是 .

查看答案和解析>>
科目:初中数学 来源:2017届湖北鄂州鄂城区九年级上期末数学试卷(解析版) 题型:单选题
函数y= 与y=﹣kx2+k(k≠0)在同一直角坐标系中的图象可能是( )
与y=﹣kx2+k(k≠0)在同一直角坐标系中的图象可能是( )
A.  B.
B. 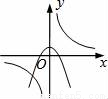 C.
C.  D.
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com