
 近几年来,石家庄市区的环境越来越美,随处可见的街心花园成为人们休闲的好去处,现二环路办事处又计划将十字路口附近的小块土地进行绿化改造,他们依地势整理出一块矩形区域ABCD,铺成人们可以活动的砖石地面,又分别以AB、BC、CD、DA为斜边向外做等腰直角三角形(如图所示),通过测量,发现四边形MNGH的周长正好是200米,设AB=x米,BC=y米.
近几年来,石家庄市区的环境越来越美,随处可见的街心花园成为人们休闲的好去处,现二环路办事处又计划将十字路口附近的小块土地进行绿化改造,他们依地势整理出一块矩形区域ABCD,铺成人们可以活动的砖石地面,又分别以AB、BC、CD、DA为斜边向外做等腰直角三角形(如图所示),通过测量,发现四边形MNGH的周长正好是200米,设AB=x米,BC=y米.分析 (1)根据矩形的判定定理证明四边形MNGH为矩形,根据等腰直角三角形的性质证明MH=MN,得到四边形MNGH为正方形;
(2)根据AB=x米,BC=y米和等腰三角形的性质求出MA和AH,根据四边形MNGH的周长是200米,求出边长,列式求出y与x之间的函数关系式;
(3)用x、y表示出总建设费用p,把y=-x+50$\sqrt{2}$代入整理,得到p(元)与x(米)之间的函数关系式;
(4)根据二次函数的性质求出函数的最小值,得到答案.
解答 解:(1)∵以AB、BC、CD、DA为斜边向外做等腰直角三角形,
∴四边形MNGH为矩形,
∵AB=CD,△AHB和△CND为等腰直角三角形,
∴AH=DN,又MA=MD,
∴MH=MN,
∴四边形MNGH为正方形;
(2)∵AB=x,
∴BH=$\frac{\sqrt{2}}{2}$x,
∵BC=y,
∴BG=$\frac{\sqrt{2}}{2}$y,
∴$\frac{\sqrt{2}}{2}$x+$\frac{\sqrt{2}}{2}$y=200÷4,
整理得y=-x+50$\sqrt{2}$;
(3)P=50xy+(502-xy)×100
=-50xy+250000
=-50(-x+50$\sqrt{2}$)+250000
=50x2-2500$\sqrt{2}$x+250000.
(4)当x=$\frac{-2500\sqrt{2}}{2×50}$时,P有最小值,
P最小值=$\frac{4×50×250000-(-2500\sqrt{2})^{2}}{4×50}$=187500.
则最少投入187500元,才能完成此项工程.
故答案为:正方形;y=-x+50$\sqrt{2}$.
点评 本题考查的是正方形的性质和二次函数的性质,正确运用数形结合思想列出函数关系式是解题的关键,注意二次函数的性质的运用.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源:2017届湖北省赤壁市九年级下学期第一次模拟(调研)考试数学试卷(解析版) 题型:填空题
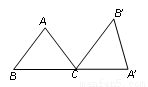
如图,在△ABC中,AB=AC =5,BC=6,将△ABC绕点C顺时针方向旋转一定角度后得到△A′B′C,若点A′恰好落在BC的延长线上,则点B′到BA′的距离为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
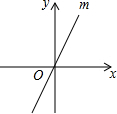 如图,在平面直角坐标系中,直线m经过原点,且与x轴正半轴成60度的角.若点N到x轴、直线m的距离分别为2和1,则点N的坐标为(0,2)或(0,-2)或($\frac{4\sqrt{3}}{3}$,2)或(-$\frac{4\sqrt{3}}{3}$,-2).
如图,在平面直角坐标系中,直线m经过原点,且与x轴正半轴成60度的角.若点N到x轴、直线m的距离分别为2和1,则点N的坐标为(0,2)或(0,-2)或($\frac{4\sqrt{3}}{3}$,2)或(-$\frac{4\sqrt{3}}{3}$,-2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com