·ÖĪö£ŗ£Ø1£©Éč³ö“ĖÅ×ĪļĻߵĽāĪöŹ½£¬°ŃA”¢BĮ½µćµÄ×ų±ź“śČė“Ė½āĪöŹ½Ēó³öa”¢bµÄÖµ¼“æÉ£»
£Ø2£©ÓÉÓėtµÄȔֵ·¶Ī§²»ÄÜČ·¶Ø£¬¹ŹÓ¦·ÖČżÖÖĒéæö½ųŠŠĢÖĀŪ£¬
¢Łµ±0£¼t”Ü2£¬ÖŲµž²æ·ÖµÄĆ껿ŹĒS
”÷OPQ£¬¹żµćA×÷AF”ĶxÖįÓŚµćF£¬ŌŚRt”÷OPQÖŠĄūÓĆČż½ĒŠĪµÄĆ껿¹«Ź½¼°ĢŲŹā½ĒµÄČż½ĒŗÆŹżÖµ¼“æÉĒó³öĘäĆ껿£»
¢Śµ±2£¼t”Ü3£¬ÉčPQ½»ABÓŚµćG£¬×÷GH”ĶxÖįÓŚµćH£¬”ĻOPQ=”ĻQOP=45”ć£¬ŌņĖıߊĪOAGPŹĒµČŃüĢŻŠĪ£¬
ÖŲµž²æ·ÖµÄĆ껿ŹĒS
ĢŻŠĪOAGP£¬ÓÉĢŻŠĪµÄĆ껿¹«Ź½¼“æÉĒó½ā£»
¢Ūµ±3£¼t£¼4£¬ÉčPQÓėAB½»ÓŚµćM£¬½»BCÓŚµćN£¬ÖŲµž²æ·ÖµÄĆ껿ŹĒS
Īå±ßŠĪOAMNC£®
ŅņĪŖ”÷PNCŗĶ”÷BMN¶¼ŹĒµČŃüÖ±½ĒČż½ĒŠĪ£¬ĖłŅŌÖŲµž²æ·ÖµÄĆ껿ŹĒS
Īå±ßŠĪOAMNC=S
ĢŻŠĪOABC-S
”÷BMN£¬½ų¶ųæÉĒó³ö“š°ø£»
£Ø3£©ĄūÓĆŅŃÖŖµĆ³ö”ĻBAO=”ĻQPC£¬Ö»ŅŖ
=
»ņÕß
=
¼“æÉµĆ³öŅŌC”¢P”¢QĪŖ¶„µćµÄČż½ĒŠĪÓė”÷OABĻąĖĘ£¬½ų¶ųĒó³ö¼“æÉ£»
£Ø4£©øł¾ŻĶ¼ŠĪŠż×ŖµÄŠŌÖŹæÉĒó³ö½«”÷OPQČĘ×ŵćPĖ³Ź±ÕėŠż×Ŗ90”揱P”¢QĮ½µćµÄ×ų±ź£¬ŌŁøł¾ŻÅ×ĪļĻߵĽāĪöŹ½¼“æÉĒó³ötµÄÖµ£®
½ā“š£ŗ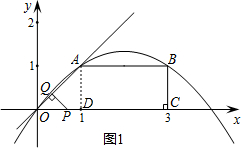
½ā£ŗ£Ø1£©ÉčÅ×ĪļĻß½āĪöŹ½ĪŖy=ax
2+bx£Øa”Ł0£©£¬½«A£®Bµć×ų±ź“śČėµĆ³ö£ŗ
£¬
½āµĆ£ŗ
£¬
¹Ź¾¹żO”¢A”¢BČżµćµÄÅ×ĪļĻß½āĪöŹ½ĪŖ£ŗy=-
x
2+
x£®
£Ø2£©¢Łµ±0£¼t”Ü2Ź±£¬ÖŲµž²æ·ÖĪŖ”÷OPQ£¬¹żµćA×÷AD”ĶxÖįÓŚµćD£¬
ČēĶ¼1£®
ŌŚRt”÷AODÖŠ£¬AD=OD=1£¬”ĻAOD=45”ć£®
ŌŚRt”÷OPQÖŠ£¬OP=t£¬”ĻOPQ=”ĻQOP=45”ć£®
”ąOQ=PQ=
t£®
”ąS=S
”÷OPQ=
OQ•PQ=
”Į
t”Į
t=
t
2£Ø0£¼t”Ü2£©£»
¢Śµ±2£¼t”Ü3Ź±£¬ÉčPQ½»ABÓŚµćE£¬ÖŲµž²æ·ÖĪŖĢŻŠĪAOPE£¬
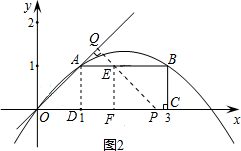
×÷EF”ĶxÖįÓŚµćF£¬ČēĶ¼2£®”ß”ĻOPQ=”ĻQOP=45”ć
”ąĖıߊĪAOPEŹĒµČŃüĢŻŠĪ”ąAE=DF=t-2£®
”ąS=S
ĢŻŠĪAOPE=
£ØAE+OP£©•AD=
£Øt-2+t£©”Į1
=t-1£Ø2£¼t”Ü3£©£»
¢Ūµ±3£¼t£¼4Ź±£¬ÉčPQ½»ABÓŚµćE£¬½»BCÓŚµćF£¬
ÖŲµž²æ·ÖĪŖĪå±ßŠĪAOCFE£¬ČēĶ¼3£®
”ßB£Ø3£¬1£©£¬OP=t£¬”ąPC=CF=t-3£®
”ß”÷PFCŗĶ”÷BEF¶¼ŹĒµČŃüÖ±½ĒČż½ĒŠĪ
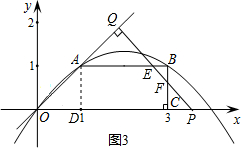
”ąBE=BF=1-£Øt-3£©=4-t
”ąS=S
Īå±ßŠĪAOCFE=S
ĢŻŠĪOABC-S
”÷BEF£¬
=
£Ø2+3£©”Į1-
£Ø4-t£©
2=-
t
2+4t-
£Ø3£¼t£¼4£©£»
£Ø3£©Į¬½ÓQC£¬OB£¬
”ßAB”ĪOC£¬
”ą”ĻBAO+”ĻAOC=180”ć£¬
”ß”ĻAOC=45”ć£¬”ĻOQP=90”ć£¬
”ą”ĻQPO=45”ć£¬
”ß”ĻQPO+”ĻQPC=180”ć£¬
”ą”ĻBAO=”ĻQPC£¬
Ö»ŅŖ
=
»ņÕß
=
¼“æÉµĆ³öŅŌC”¢P”¢QĪŖ¶„µćµÄČż½ĒŠĪÓė”÷OABĻąĖĘ£¬
µĆ³ö£ŗ3-t=
”Į
t »ņ3-t=
”Į
t
½āµĆ£ŗt=2»ņt=
£»
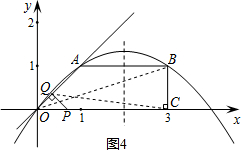
£Ø4£©“ęŌŚ£¬t
1=1£¬t
2=2£®
½«”÷OPQČĘ×ŵćPĖ³Ź±ÕėŠż×Ŗ90”ć£¬“ĖŹ±Q£Øt+
£¬
£©£¬O£Øt£¬t£©
¢Łµ±µćQŌŚÅ×ĪļĻßÉĻŹ±£¬
=-
”Į£Øt+
£©
2+
”Į£Øt+
£©£¬
½āµĆt=2£»
¢Śµ±µćOŌŚÅ×ĪļĻßÉĻŹ±£¬t=-
t
2+
t£¬
½āµĆ£ŗt=1£®

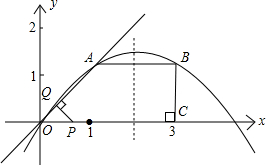
 ČēĶ¼ĖłŹ¾£¬ŅŃÖŖŌŚÖ±½ĒĢŻŠĪOABCÖŠ£¬AB”ĪOC£¬BC”ĶxÖįÓŚµćC£¬A£Ø1£¬1£©”¢B£Ø3£¬1£©£®¶ÆµćP“ÓOµć³ö·¢£¬ŃŲxÖįÕż·½ĻņŅŌĆæĆė1øöµ„Ī»³¤¶ČµÄĖŁ¶ČŅĘ¶Æ£®¹żPµć×÷PQ“¹Ö±ÓŚÖ±ĻßOA£¬“¹×ćĪŖQ£®ÉčPµćŅĘ¶ÆµÄŹ±¼äĪŖtĆė£Ø0£¼t£¼4£©£¬”÷OPQÓėÖ±½ĒĢŻŠĪOABCÖŲµž²æ·ÖµÄĆ껿ĪŖS£®
ČēĶ¼ĖłŹ¾£¬ŅŃÖŖŌŚÖ±½ĒĢŻŠĪOABCÖŠ£¬AB”ĪOC£¬BC”ĶxÖįÓŚµćC£¬A£Ø1£¬1£©”¢B£Ø3£¬1£©£®¶ÆµćP“ÓOµć³ö·¢£¬ŃŲxÖįÕż·½ĻņŅŌĆæĆė1øöµ„Ī»³¤¶ČµÄĖŁ¶ČŅĘ¶Æ£®¹żPµć×÷PQ“¹Ö±ÓŚÖ±ĻßOA£¬“¹×ćĪŖQ£®ÉčPµćŅĘ¶ÆµÄŹ±¼äĪŖtĆė£Ø0£¼t£¼4£©£¬”÷OPQÓėÖ±½ĒĢŻŠĪOABCÖŲµž²æ·ÖµÄĆ껿ĪŖS£® ½ā£ŗ£Ø1£©ÉčÅ×ĪļĻß½āĪöŹ½ĪŖy=ax2+bx£Øa”Ł0£©£¬½«A£®Bµć×ų±ź“śČėµĆ³ö£ŗ
½ā£ŗ£Ø1£©ÉčÅ×ĪļĻß½āĪöŹ½ĪŖy=ax2+bx£Øa”Ł0£©£¬½«A£®Bµć×ų±ź“śČėµĆ³ö£ŗ





 0£¼t£¼4£©£¬”÷OPQÓėÖ±½ĒĢŻŠĪOABCÖŲµž²æ·ÖµÄĆ껿ĪŖS£®
0£¼t£¼4£©£¬”÷OPQÓėÖ±½ĒĢŻŠĪOABCÖŲµž²æ·ÖµÄĆ껿ĪŖS£® Ö±ÓŚÖ±ĻßOA£¬“¹×ćĪŖQ£¬ÉčPµćŅĘ¶ÆµÄŹ±¼äĪŖtĆė£Ø0£¼t£¼4£©£¬”÷OPQÓėÖ±½ĒĢŻŠĪOABCÖŲµž²æ·ÖµÄĆ껿ĪŖS£®
Ö±ÓŚÖ±ĻßOA£¬“¹×ćĪŖQ£¬ÉčPµćŅĘ¶ÆµÄŹ±¼äĪŖtĆė£Ø0£¼t£¼4£©£¬”÷OPQÓėÖ±½ĒĢŻŠĪOABCÖŲµž²æ·ÖµÄĆ껿ĪŖS£®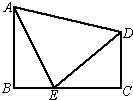 6”¢ČēĶ¼ĖłŹ¾£¬ŅŃÖŖŌŚÖ±½ĒĢŻŠĪABCDÖŠ£¬”ĻB=”ĻC=90”ć£¬EĪŖBCÉĻµÄµć£¬ĒŅEA=ED£¬”ĻAEB=75”ć£¬”ĻDEC=45”ć£¬ŹŌĖµĆ÷AB=BC£®
6”¢ČēĶ¼ĖłŹ¾£¬ŅŃÖŖŌŚÖ±½ĒĢŻŠĪABCDÖŠ£¬”ĻB=”ĻC=90”ć£¬EĪŖBCÉĻµÄµć£¬ĒŅEA=ED£¬”ĻAEB=75”ć£¬”ĻDEC=45”ć£¬ŹŌĖµĆ÷AB=BC£® ČēĶ¼ĖłŹ¾£¬ŅŃÖŖŌŚÖ±½ĒČż½ĒŠĪÖ½Ę¬ABCÖŠ£¬BC=3£¬”ĻBAC=30”ć£¬ŌŚACÉĻČ”Ņ»µćE£¬ŅŌBEĪŖÕŪŗŪ£¬Ź¹ABµÄŅ»²æ·ÖÓėBCÖŲŗĻ£¬AÓėBCŃÓ³¤ĻßÉĻµÄµćDÖŲŗĻ£¬ŌņDEµÄ³¤¶ČĪŖ£Ø””””£©
ČēĶ¼ĖłŹ¾£¬ŅŃÖŖŌŚÖ±½ĒČż½ĒŠĪÖ½Ę¬ABCÖŠ£¬BC=3£¬”ĻBAC=30”ć£¬ŌŚACÉĻČ”Ņ»µćE£¬ŅŌBEĪŖÕŪŗŪ£¬Ź¹ABµÄŅ»²æ·ÖÓėBCÖŲŗĻ£¬AÓėBCŃÓ³¤ĻßÉĻµÄµćDÖŲŗĻ£¬ŌņDEµÄ³¤¶ČĪŖ£Ø””””£©