
【题目】苏州地处太湖之滨,有丰富的水产养殖资源,水产养殖户李大爷准备进行大闸蟹与河虾的混合养殖,他了解到如下信息:
①每亩水面的年租金为500元,水面需按整数亩出租;
②每亩水面可在年初混合投放4公斤蟹苗和20公斤虾苗;
③每公斤蟹苗的价格为75元,其饲养费用为525元,当年可获1 400元收益;
④每公斤虾苗的价格为15元,其饲养费用为85元,当年可获160元收益;
(1)若租用水面n亩,则年租金共需__________元;
(2)水产养殖的成本包括水面年租金、苗种费用和饲养费用,求每亩水面蟹虾混合养殖的年利润(利润=收益-成本);
(3)李大爷现在资金25 000元,他准备再向银行贷不超过25 000元的款,用于蟹虾混合养殖.已知银行贷款的年利率为8%,试问李大爷应该租多少亩水面,并向银行贷款多少元,可使年利润超过35 000元?
【答案】(1)500n;(2)3900;(3)24000元.
【解析】试题分析:(1)根据年租金=每亩水面的年租金×亩数求解即可;
(2)年利润=收益-成本=(蟹苗收益+虾苗收益)-(蟹苗成本+虾苗成本)-水面年租金-饲养总费用;
(3)设应该租n亩水面,根据贷款不超过25000,年利润超过35000列出不等式组,结合题意求出n的值.
(1)若租用水面n亩,则年租金共需500n元;
(2)每亩收益=4×1400+20×160=8800
每亩成本=4×(75+525)+20×(15+85)+500=4900
利润=8800-4900=3900;
(3)设租n亩,则贷款(4900n-25000)元,由题意得
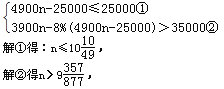
又∵n为正整数
∴n="10"
∴贷款4900×10-25000=24000(元).


科目:初中数学 来源: 题型:
【题目】如图,线段AB是⊙O的直径,BC⊥CD于点C,AD⊥CD于点D,请仅用无刻度的直尺按下列要求作图.
(1)在图1中,当线段CD与⊙O相切时,请在CD上确定一点E,连接BE,使BE平分∠ABC;
(2)在图2中,当线段CD与⊙O相离时,请过点O作OF⊥CD,垂足为F.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中共十九大召开期间,十九大代表纷纷利用休息时间来到北京展览馆,参观“砥砺奋进的五年”大型成就展,据统计,9月下旬开幕至10月22日,展览累计参观人数已经超过78万,请将780000用科学记数法表示为( )
A. 78×104 B. 7.8×105 C. 7.8×106 D. 0.78×106
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列表述中,正确的是( )
A. 有理数有最大的数,也有最小的数
B. 有理数有最大的数,但没有最小的数
C. 有理数有最小的数,但没有最大的数
D. 有理数既没有最大的数,也没有最小的数
查看答案和解析>>
科目:初中数学 来源: 题型:
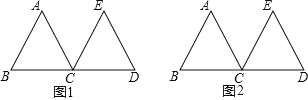
【题目】如图,等边△ABC和等边△ECD的边长相等,BC与CD两边在同一直线上,请根据如下要求,使用无刻度的直尺,通过连线的方式画图.
(1)在图1中画出一个直角三角形.(2)在图2中过点C作BD的垂线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知射线AB与直线CD交于点O,OF平分∠BOC,OG⊥OF于O,AE∥OF,且∠A=30°. 
(1)求∠DOF的度数;
(2)试说明OD平分∠AOG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ABC=2∠ACB,延长AB至点D,使BD=BC,点E是直线BC上一点,点F是直线AC上一点,连接DE.连接EF,且∠DEF=∠DBC.
(1)如图1,若∠D=∠EFC=15°,AB=![]() ,求AC的长.
,求AC的长.
(2)如图2,当∠BAC=45°,点E为线段BC的延长线上,点F在线段AC的延长线上时,求证:CF=![]() BE.
BE.
(3)如图3,当∠BAC=90°,点E为线段CB的延长线上,点F在线段CA的延长线上时,猜想线段CF与线段BE的数量关系,并证明猜想的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙、丁四位选手各射击10次,每人的平均成绩都是9.3环,方差如表:
选手 | 甲 | 乙 | 丙 | 丁 |
方差(环2) | 0.035 | 0.016 | 0.022 | 0.025 |
则这四个人种成绩发挥最稳定的是( )
A.甲B.乙C.丙D.丁
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com