
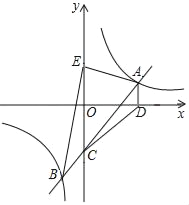
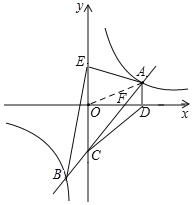
【题目】如图,一次函数y=kx+b(k≠0)的图象与反比例函数y=![]() (m≠0)的图象交于点A、B,与y轴交于点C.过点A作AD⊥x轴于点D,AD=2,∠CAD=45°,连接CD,已知△ADC的面积等于6.
(m≠0)的图象交于点A、B,与y轴交于点C.过点A作AD⊥x轴于点D,AD=2,∠CAD=45°,连接CD,已知△ADC的面积等于6.
(1)求一次函数和反比例函数的解析式;
(2)若点E是点C关于x轴的对称点,求△ABE的面积.
【答案】(1)y=x﹣4,y=![]() ;(2)32
;(2)32
【解析】
(1)依据S△AOD=S△ADC=6,可得A(6,2),将A(6,2)代入![]() ,可得到反比例函数解析式;将点A(6,2),点C(0,﹣4)代入y=kx+b,可得一次函数解析式;
,可得到反比例函数解析式;将点A(6,2),点C(0,﹣4)代入y=kx+b,可得一次函数解析式;
(2)依据E(0,4),可得CE=8,解方程组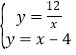 ,即可得到B(﹣2,﹣6),进而得出△ABE的面积.
,即可得到B(﹣2,﹣6),进而得出△ABE的面积.
(1)连接AO.
∵AD⊥x轴于点D,设A(a,2),∴AD=2.
∵∠CAD=45°,∴∠AFD=45°,∴FD=AD=2.
∵AD∥y轴,∴S△AOD=S△ADC=6,∴OD=6,∴A(6,2),将A(6,2)代入![]() ,得:m=12,∴反比例函数解析式为y
,得:m=12,∴反比例函数解析式为y![]() ;
;
∵∠OCF=∠CAD=45°.在△COF中,OC=OF=OD﹣FD=6﹣2=4,∴C(0,﹣4),将点A(6,2),点C(0,﹣4)代入y=kx+b,可得:
![]() ,∴
,∴![]() ,∴一次函数解析式为y=x﹣4;
,∴一次函数解析式为y=x﹣4;
(2)点E是点C关于x轴的对称点,∴E(0,4),∴CE=8,解方程组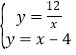 ,得:
,得:![]() 或
或![]() ,∴B(﹣2,﹣6),∴
,∴B(﹣2,﹣6),∴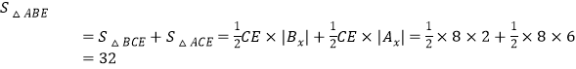 .
.


科目:初中数学 来源: 题型:
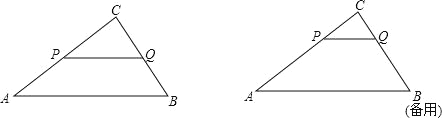
【题目】如图:已知△ABC中,AB=5,BC=3,AC=4,PQ∥AB,P点在AC上(与A、C不重合),Q在BC上.
(1)当△PQC的面积与四边形PABQ的面积相等时,求CP的长;
(2)当△PQC的周长与四边形PABQ的周长相等时,求CP的长;
(3)试问:在AB上是否存在一点M,使得△PQM为等腰直角三角形?若不存在,请简要说明理由;若存在,请求出PQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
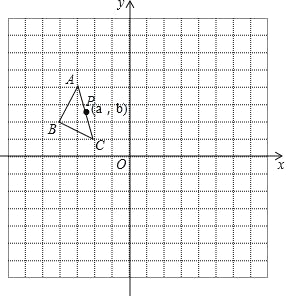
【题目】如图,在平面直角坐标系中有△ABC,其中A(﹣3,4),B(﹣4,2),C(﹣2,1).把△ABC绕原点顺时针旋转90°,得到△A1B1C1.再把△A1B1C1向左平移2个单位,向下平移5个单位得到△A2B2C2.
(1)画出△A1B1C1和△A2B2C2.
(2)直接写出点B1、B2坐标.
(3)P(a,b)是△ABC的AC边上任意一点,△ABC经旋转平移后P对应的点分别为P1、P2,请直接写出点P1、P2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了测量某风景区内一座塔AB的高度,小明分别在塔的对面一楼房CD的楼底C、楼顶D处,测得塔顶A的仰角为45°和30°,已知楼高CD为10m,求塔的高度.(sin30°=0.50,cos30°≈0.87,tan30°≈0.58)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种蔬菜每千克售价![]() (元)与销售月份
(元)与销售月份![]() 之间的关系如图1所示,每千克成本
之间的关系如图1所示,每千克成本![]() (元)与销售月份
(元)与销售月份![]() 之间的关系如图2所示,其中图1中的点在同一条线段上,图2中的点在同一条抛物线上,且抛物线的最低点的坐标为(6,1).
之间的关系如图2所示,其中图1中的点在同一条线段上,图2中的点在同一条抛物线上,且抛物线的最低点的坐标为(6,1).
(1)求出![]() 与
与![]() 之间满足的函数表达式,并直接写出
之间满足的函数表达式,并直接写出![]() 的取值范围;
的取值范围;
(2)求出![]() 与
与![]() 之间满足的函数表达式;
之间满足的函数表达式;
(3)设这种蔬菜每千克收益为![]() 元,试问在哪个月份出售这种蔬菜,
元,试问在哪个月份出售这种蔬菜,![]() 将取得最大值?并求出此最大值.(收益=售价-成本)
将取得最大值?并求出此最大值.(收益=售价-成本)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春秋旅行社为吸引市民组团去天水湾风景区旅游,推出了如下收费标准:
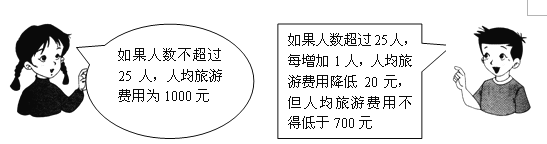 某单位组织员工去天水湾风景区旅游,共支付给春秋旅行社旅游费用27000元,请问该单位这次共有多少员工去天水湾风景区旅游?
某单位组织员工去天水湾风景区旅游,共支付给春秋旅行社旅游费用27000元,请问该单位这次共有多少员工去天水湾风景区旅游?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某次模拟考试后,抽取 m 名学生的数学成绩进行整理分组,形成如下表格(x 代表成绩),并绘制出扇形统计图和频数分布直方图(横坐标表示成绩,单位:分).
A 组 | 140<x≤150 |
B 组 | 130<x≤140 |
C 组 | 120<x≤130 |
D 组 | 110<x≤120 |
E 组 | 100<x≤110 |
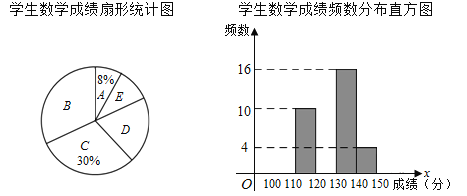
(1)m 的值为多少,扇形统计图中 D 组对应的圆心角是多少度.
(2)请补全条形统计图,并标注出相应的人数.
(3)若此次考试数学成绩 130 分以上的为优秀,参加此次模拟考的学生总数为 2000,请估算此次考试数学成绩优秀的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】分别写一个满足下列条件的一元二次方程:
方程的两个根相等___________________________________
方程的两根互为相反数______________________________________
方程的两根互为倒数__________________________________________
查看答案和解析>>
科目:初中数学 来源: 题型:
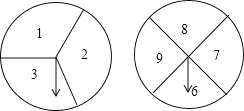
【题目】如图是两个可以自由转动的转盘,甲转盘被等分成3个扇形,乙转盘被等分成4个扇形,每一个扇形上都标有相应的数字![]() 小强和小宁利用它们做游戏,游戏规则是:同时转动两个转盘,当转盘停止后,指针所指区域内的两数字之和小于9,小宁获胜;指针所指区域内的两数字之和等于9为平局;指针所指区域内的两数字之和大于9,小强获胜
小强和小宁利用它们做游戏,游戏规则是:同时转动两个转盘,当转盘停止后,指针所指区域内的两数字之和小于9,小宁获胜;指针所指区域内的两数字之和等于9为平局;指针所指区域内的两数字之和大于9,小强获胜![]() 如果指针恰好指在分割线上,那么重转一次.
如果指针恰好指在分割线上,那么重转一次.
![]() 画树状图表示所有可能出现的结果,并指出小宁获胜的概率;
画树状图表示所有可能出现的结果,并指出小宁获胜的概率;
![]() 该游戏规则对小宁,小强是否公平?如公平,请说明理由,如不公平,请修改游戏规则,使游戏公平.
该游戏规则对小宁,小强是否公平?如公平,请说明理由,如不公平,请修改游戏规则,使游戏公平.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com