
【题目】先阅读下面的内容,再解决问题,
例题:若![]() ,求
,求![]() 和
和![]() 的值.
的值.
解:∵![]()
∴![]()
∴![]() ∴
∴![]()
∴![]()
问题(1)若△ABC的三边长![]() 都是正整数,且满足
都是正整数,且满足![]() ,请问△ABC是什么形状?说明理由.
,请问△ABC是什么形状?说明理由.
(2)若![]() ,求
,求![]() 的值.
的值.
(3)已知![]() ,则
,则![]() .
.
【答案】(1)△ABC是等边三角形,理由见解析;(2)![]() ;(3)3
;(3)3
【解析】(1)先把a2+b2-6a-6b+18+|3-c|=0,配方得到(a-3)2+|3-c|=0,根据非负数的性质得到a=b=c=3,得出三角形的形状即可;
(2)首先把x2+4x2-2xy+12y+12=0,配方得到(x-y)2+3(y+2)2=0,再根据非负数的性质得到x=-2,代入求得值即可;
(3)首先根据a-b=8,ab+c2-16c+80=0,应用因式分解的方法,判断出(a-4)2+(c-8)2=0,求出A、B、C的值各是多少;然后把a、b、c的值求和,求出a+b+c的值是多少即可.
解:(1)△ABC是等边三角形
由题意得![]()
∴![]() ∴△ABC是等边三角形.
∴△ABC是等边三角形.
(2)由题意得![]()
∴![]() .
.
∴![]() .
.
(3)∵a–![]() b=4,即a=b+4,(b+4)b+c2–6c+13=0,
b=4,即a=b+4,(b+4)b+c2–6c+13=0,
∴(b2+4b+4)+(c2–6c+9)=0,
∴b+2=0,c–3=0,
∴b = –2,c =3,a =2,
∴a+b+c=3.
“点睛”此题主要考查了因式分解的应用,要熟练掌握,解答此题的关键是要明确:用因式分解的方法将式子变形时,关键一招条件,变形的可以是整个代数式,也可以是其中的一部分.此题还考查了三角形的三条边之间的关系,要熟练掌握,解答此题的关键是要明确:任意两边之和大于弟三边;任意两边之差小于第三边.


科目:初中数学 来源: 题型:
【题目】已知A、B两地相距30 km,小明以6 km/h的速度从A步行到B地的距离为ykm,步行的时间为xh.求y与x之间的函数表达式,并指出y是x的什么函数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,点M、N分别在AB、BC上,将BMN沿MN翻折,得FMN,若MF∥AD,FN∥DC,则∠D的度数为_________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,假命题是( )
A. 对角线互相平分的四边形是平行四边形
B. 对角线互相平分且相等的四边形是矩形
C. 对角线互相垂直平分的四边形是菱形
D. 对角线互相垂直且相等的四边形是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(a,1)与点A′(5,b)关于坐标原点对称,则实数a、b的值是( )
A.a=5,b=1 B.a=-5,b=1
C.a=5,b=-1 D.a=-5,b=-1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从A地将一批物品运往B地,再返回A地,图6表示两车离A地的距离s(千米)随时间t(小时)变化的图象,已知乙车到达B地后以30千米/小时的速度返回.请根据图象中的数据回答:

(1)甲车出发多长时间后被乙车追上?
(2)甲车与乙车在距离A地多远处迎面相遇?
(3)甲车从B地返回的速度多大时,才能比乙车先回到A地?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按图填空, 并注明理由
已知: 如图, ∠1=∠2, ∠3=∠E. 求证: AD∥BE
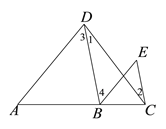
证明: ∵∠1 = ∠2 (已知)
∴ ∥ ( )
∴ ∠E = ∠ ( )
又∵ ∠E = ∠3 ( 已知 )
∴ ∠3 = ∠ ( 等量代换 )
∴ ∥ ( 内错角相等,两直线平行 )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com