解:(1)①连接OC,
∵∠A=45゜,
∴∠EOF=2∠A=90°,
∴∠AOE+∠BOF=90°,
∵CA=CB,O为AB的中点,
∴CO⊥AB,OA=OB,∠A=∠B=45°,
∴OC=OA=OB=

AB,∠BOC=∠A=45°,
∴∠BOF+∠COF=90°,
∴∠AOE=∠COF,
在△AOE和△COF中,
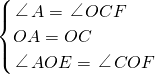
,
∴△AOE≌△COF(ASA),
∴OE=OF,CF=AE,
∴

=1;
②∵CF=AE,
∴AC=AE+CE=CF+CE,
∴
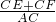
=1;
(2)①连接OC,
∵∠A=45゜,
∴∠EOF=2∠A=90°,
∴∠AOE+∠BOF=90°,
∵CA=CB,O为AB的中点,
∴CO⊥AB,OA=OB,∠A=∠B=45°,
∴OC=OA=OB=

AB,∠BOC=∠A=45°,
∴∠BOF+∠COF=90°,
∴∠AOE=∠COF,
在△AOE和△COF中,
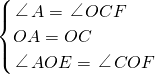
,
∴△AOE≌△COF(ASA),
∴OE=OF,CF=AE,
②∴CF-CE=AE-CE=AC;
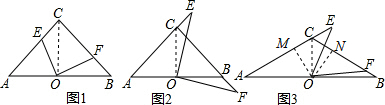
(3)CF-CE=

AC.
理由:连接OC,过点O作OM⊥AE于 M,ON⊥CF于N,
∵CA=CB,O为AB的中点,
∴OM=ON,∠ACO=∠BCO,CO⊥AB,
∴∠COM=∠CON,
∴CM=CN,
∵∠A=30°,
∴∠EOF=2∠A=60°,∠B=∠A=30°,OC=

AC,
∴∠ACB=120°,
∴∠MON=60°,
∴∠MON=∠EOF=30°,
∴∠EOM=∠FON,CM=

OC,
在△EOM和△FON中,
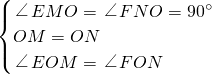
,
∴△EOM≌△FON(ASA),
∴EM=NF,
∴CF-CE=CN+NF-CE=CM+ME-CE=CM+CM=2CM=OC=

AC.
分析:(1)首先连接OC,易证得△AOC与△BOC是等腰直角三角形,继而证得△AOE≌△COF,则可证得OE=OF,CF=AE,则可证得
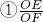
=1;
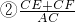
=1;
(2)首先连接OC,易证得△AOC与△BOC是等腰直角三角形,继而证得△AOE≌△COF,则可证得OE=OF,CF=AE,继而可得CF-CE=AC;
(3)首先OC,作OM⊥AE于 M,ON⊥CF于N,则可得△COM≌△CON,△EOM≌△FON,即可得CM=CN,EM=NF,继而可得CF-CE=

AC.
点评:此题考查了全等三角形的判定与性质、等腰直角三角形的性质以及含30°角的直角三角形的性质.此题难度较大,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

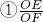 =1;
=1;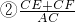 =1;
=1;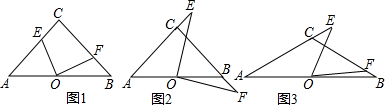
 AB,∠BOC=∠A=45°,
AB,∠BOC=∠A=45°,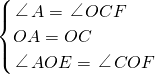 ,
, =1;
=1;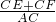 =1;
=1; AB,∠BOC=∠A=45°,
AB,∠BOC=∠A=45°,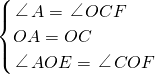 ,
,
 AC.
AC. AC,
AC, OC,
OC,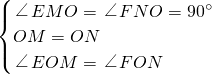 ,
, AC.
AC.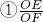 =1;
=1;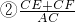 =1;
=1; AC.
AC.

 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案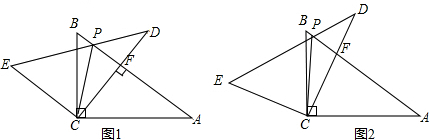
 8、如图,已知在△ABC中,AD垂直平分BC,AC=EC,点B、D、C、E在同一直线上,则下列结论:①AB=AC;②∠CAE=∠E;③AB+BD=DE;④∠BAC=∠ACB.正确的个数有( )个.
8、如图,已知在△ABC中,AD垂直平分BC,AC=EC,点B、D、C、E在同一直线上,则下列结论:①AB=AC;②∠CAE=∠E;③AB+BD=DE;④∠BAC=∠ACB.正确的个数有( )个.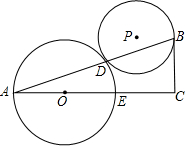 外切于点D,若AC和BC边的长是关于x的方程x2-(AB+4)x+4AB+8=0的两根,且25BC•sinA=9AB,
外切于点D,若AC和BC边的长是关于x的方程x2-(AB+4)x+4AB+8=0的两根,且25BC•sinA=9AB,