
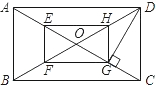
 如图,O是矩形ABCD的对角线的交点,E,F,G,H分别是OA,OB,OC,OD的中点;
如图,O是矩形ABCD的对角线的交点,E,F,G,H分别是OA,OB,OC,OD的中点;分析 (1)首先证明四边形EFGH是平行四边形,然后再证明HF=EG;
(2)根据题干求出矩形的边长CD和BC,然后根据矩形面积公式求得.
解答 (1) 证明:∵四边形ABCD是矩形,
证明:∵四边形ABCD是矩形,
∴OA=0B=OC=OD,
∵AE=BF=CG=DH,
∴AO-AE=OB-BF=CO-CG=DO-DH,
即:OE=OF=OG=OH,
∴四边形EFGH是矩形;
(2)解:∵G是OC的中点,
∴GO=GC,
∵DG⊥AC,
∴∠DGO=∠DGC=90°,
又∵DG=DG,
∴△DGC≌△DGO,
∴CD=OD,
∵F是BO中点,OF=2cm,
∴BO=4cm,
∵四边形ABCD是矩形,
∴DO=BO=4cm,
∴DC=4cm,DB=8cm,
∴CB=$\sqrt{B{D}^{2}-D{C}^{2}}$=4$\sqrt{3}$,
∴矩形ABCD的面积=4×4$\sqrt{3}$=16$\sqrt{3}$cm2.
点评 本题主要考查矩形的判定,首先要判定四边形是平行四边形,然后证明对角线相等.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知直线y=-2x+2分别与x轴,y轴交于点C,B,并且与某一反比例函数y=$\frac{m}{x}$在第二象限交于点A(-1,a),过点B作直线AC的垂线交x轴于点E,交另一双曲线y=$\frac{n}{x}$于点D(b,-2).
已知直线y=-2x+2分别与x轴,y轴交于点C,B,并且与某一反比例函数y=$\frac{m}{x}$在第二象限交于点A(-1,a),过点B作直线AC的垂线交x轴于点E,交另一双曲线y=$\frac{n}{x}$于点D(b,-2).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 某小组在“用频率估计概率”的实验中,统计了某种结果出现的频率,绘制了如图所示的折线图,那么符合这一结果的实验最有可能的是( )
某小组在“用频率估计概率”的实验中,统计了某种结果出现的频率,绘制了如图所示的折线图,那么符合这一结果的实验最有可能的是( )| A. | 袋子中有1个红球和2个黄球,它们只有颜色上的区别,从中随机地取出一个球是黄球 | |
| B. | 掷一个质地均匀的正六面体骰子,落地时面朝上的点数是6 | |
| C. | 在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀” | |
| D. | 掷一枚质地均匀的硬币,落地时结果是“正面向上” |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,D、E分别是AB、AC的中点,过点E作EF∥AB,交BC于点F.
如图,在△ABC中,D、E分别是AB、AC的中点,过点E作EF∥AB,交BC于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com