

分析 (1)在△BEG中利用三角形内角和定理,然后根据平行线的性质可得∠AEB=∠GBE,据此即可求证;
(2)作GH⊥BE于点H,则△BGE是等腰三角形,证明△ABE∽△BGH,根据相似三角形的对应边的比相等即可求解;
(3)作BQ⊥GE于点Q,连接BF,证明△ABE≌△QBE,直角△BQF≌直角△BCF根据全等三角形的对应边相等即可证得AE+FC=EF.
解答 (1)证明:∵四边形ABCD是正方形,
∴AD∥BC,
∴∠AEB=∠GBE,
∴∠BGE=180°-∠BEG-∠GBE,即∠BGE=180°-2∠AEB.
∵∠ABE=90°-∠AEB,即2∠ABE=180°-2∠AEB,
∴∠ABE=$\frac{1}{2}$∠BGE;
(2)解:作GH⊥BE于点H.
在直角△ABE中,BE=$\sqrt{A{B}^{2}-A{E}^{2}}$=$\sqrt{29}$.
∵∠GBE=∠BEG,
∴△GBE是等腰三角形.
∴BH=EH=$\frac{1}{2}$BE=$\frac{\sqrt{29}}{2}$.
∵∠AEB=∠GBH,∠A=∠BHG=90°,
∴△ABE∽△BGH,
∴$\frac{AB}{GH}=\frac{AE}{BH}$,即$\frac{5}{GH}=\frac{2}{\frac{\sqrt{29}}{2}}$,
∴GH=$\frac{5\sqrt{29}}{4}$.
∴S△BEG=$\frac{1}{2}$BE•GH=$\frac{1}{2}$×$\sqrt{29}$×$\frac{5\sqrt{29}}{4}$=$\frac{145}{8}$;
(3)解:AE+FC=EF.
作BQ⊥GE于点Q.
在△ABE和△QBE中,
$\left\{\begin{array}{l}{∠A=∠BQE}\\{∠AEB=∠QEB}\\{BE=BE}\end{array}\right.$,
∴△ABE≌△QBE,
∴AB=QB,AE=QE,而AB=BC,
∴BQ=BC.
连接BF.
在直角△BQF和直角△BCF中,
$\left\{\begin{array}{l}{BQ=BC}\\{BF=BF}\end{array}\right.$,
∴直角△BQF≌直角△BCF,
∴QF=FC,
∴AE+FC=EQ+QF=EF.
点评 本题考查正方形的性质以及相似三角形的判定与性质以及全等三角形的判定与性质,正确作出辅助线,证明△ABE≌△QBE,直角△BQF≌直角△BCF是关键.


科目:初中数学 来源: 题型:填空题
 等边三角形ABC的顶点都在圆O上,BD为直径,则∠BDC=60°,∠ACD=30°,若CD=6cm,则△ABC的面积等于27$\sqrt{3}$cm2.
等边三角形ABC的顶点都在圆O上,BD为直径,则∠BDC=60°,∠ACD=30°,若CD=6cm,则△ABC的面积等于27$\sqrt{3}$cm2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
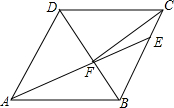 如图,在菱形ABCD中,AB=6,∠DAB=60°,AE分别交BC,BD于点E,F,CE=2,连接CF,以下结论::①△ABF≌△CBF;②点E到AB的距离是2$\sqrt{3}$;③CF=5;④△CEF的面积为$\frac{6}{5}$$\sqrt{3}$.其中一定成立的是①②④(把所有正确结论的序号都填在横线上).
如图,在菱形ABCD中,AB=6,∠DAB=60°,AE分别交BC,BD于点E,F,CE=2,连接CF,以下结论::①△ABF≌△CBF;②点E到AB的距离是2$\sqrt{3}$;③CF=5;④△CEF的面积为$\frac{6}{5}$$\sqrt{3}$.其中一定成立的是①②④(把所有正确结论的序号都填在横线上).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
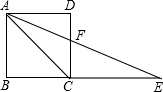 如图,正方形ABCD中,点E在BC的延长线上,AC=CE,则下列结论:
如图,正方形ABCD中,点E在BC的延长线上,AC=CE,则下列结论:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
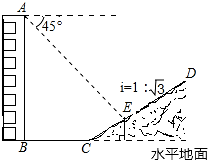 如图,一楼房AB后有一假山,其坡度为i=1:$\sqrt{3}$,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=26米,与亭子距离CE=18米,小丽从楼房顶测得E点的俯角为45°.(注:坡度i是指坡面的铅直高度与水平宽度的比)
如图,一楼房AB后有一假山,其坡度为i=1:$\sqrt{3}$,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=26米,与亭子距离CE=18米,小丽从楼房顶测得E点的俯角为45°.(注:坡度i是指坡面的铅直高度与水平宽度的比)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com