

 ≤x≤
≤x≤ 或
或 ≤x≤2
≤x≤2 ,
, ×30=20千米,
×30=20千米, ,20),表示甲、乙两人出发
,20),表示甲、乙两人出发 小时后相遇,此时距离B地20千米;
小时后相遇,此时距离B地20千米; ,
, ,
, ,
, ≤x≤
≤x≤ 或
或 ≤x≤2时,甲、乙两人能够用无线对讲机保持联系.
≤x≤2时,甲、乙两人能够用无线对讲机保持联系.

科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ,0),点B(0,2),点C是线段OA的中点.
,0),点B(0,2),点C是线段OA的中点.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 的图象在第四象限相交于点P,并且PA⊥x轴于点A,PB⊥y轴于点B,已知B(0,-6)且S△DBP=27.
的图象在第四象限相交于点P,并且PA⊥x轴于点A,PB⊥y轴于点B,已知B(0,-6)且S△DBP=27. 的图象与△ABP总有公共点,直接写出n的取值范围.
的图象与△ABP总有公共点,直接写出n的取值范围.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 与x轴相交于点A,与直线
与x轴相交于点A,与直线 相交于点P(2,
相交于点P(2,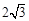 ).
).
 的形状并说明理由.
的形状并说明理由. 轴于F,EB⊥
轴于F,EB⊥ 轴于B.设运动t秒时,矩形EBOF与△OPA重叠部分的面积为S.
轴于B.设运动t秒时,矩形EBOF与△OPA重叠部分的面积为S.查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

| A.3 | B.4 | C.5 | D.6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com