
【题目】如图,Rt△ABC的内切圆⊙O与AB、BC、CA分别相切于点D、E、F,且∠ACB=90°,AB=5,BC=3,点P是边AC上的一动点,PH⊥AB,垂足为H.
(1)求⊙O的半径的长及线段AD的长;
(2)设PH=x,PC=y,求y关于x的函数关系式.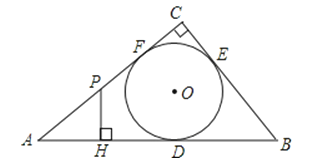
【答案】解:(1)连接AO、DO.设⊙O的半径为r.
在Rt△ABC中,由勾股定理得AC=![]() =4,
=4,
则⊙O的半径r=![]() (AC+BC﹣AB)=
(AC+BC﹣AB)=![]() (4+3﹣5)=1;
(4+3﹣5)=1;
∵CE、CF是⊙O的切线,∠ACB=90°,
∴∠CFO=∠FCE=∠CEO=90°,CF=CE,
∴四边形CEOF是正方形,
∴CF=OF=1;
又∵AD、AF是⊙O的切线,
∴AF=AD;
∴AF=AC﹣CF=AC﹣OF=4﹣1=3,
即AD=3;
(2)点P在线段AC上时.
在Rt△ABC中,AB=5,AC=4,BC=3,
∵∠C=90°,PH⊥AB,
∴∠C=∠PHA=90°,
∵∠A=∠A,
∴△AHP∽△ACB,
∴![]() ,
,
即![]()
∴y=﹣![]() x+4,
x+4,
即y与x的函数关系式是y=﹣![]() x+4.
x+4.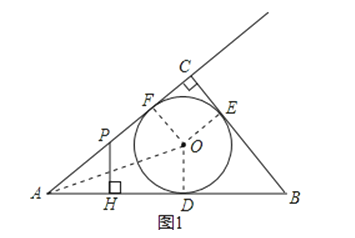
【解析】(1)由勾股定理求AC的长度;设⊙O的半径为r,则r=![]() (AC+BC﹣AB);根据圆的切线定理、正方形的判定定理知四边形CEOF是正方形;然后由正方形的性质证得CF=OF=1,则由图中线段间的和差关系即可求得AD的长度;
(AC+BC﹣AB);根据圆的切线定理、正方形的判定定理知四边形CEOF是正方形;然后由正方形的性质证得CF=OF=1,则由图中线段间的和差关系即可求得AD的长度;
(2)点P在线段AC上时,通过相似三角形△AHP∽△ACB的对应边成比例知,![]() , 将“PH=x,PC=y”代入求出即可求得y关于x的函数关系式即可.
, 将“PH=x,PC=y”代入求出即可求得y关于x的函数关系式即可.
【考点精析】通过灵活运用三角形的内切圆与内心,掌握三角形的内切圆的圆心是三角形的三条内角平分线的交点,它叫做三角形的内心即可以解答此题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD和正方形BEFG平放在一起.
(1)若两正方形的面积分别是16和9,直接写出边AE的长为 .
(2)①设正方形ABCD的边长为a,正方形BEFG的边长为b,求图中阴影部分的面积(用含a和b的代数式表示)
②在①的条件下,如果a+b=10,ab=16,求阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知平移一次函数y=2x﹣4的图象过点(﹣2,1)后的图象为l1.
(1)求图象l1对应的函数表达式,并画出图象l1;
(2)求一次函数y=﹣2x+4的图象l2与l1及x轴所围成的三角形的面积.
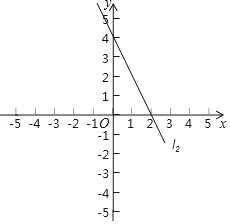
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习了“求简单随机事件发生的可能性大小”知识后,小敏,小聪,小丽三人分别编写了一道有关随机事件的试题并进行了解答.小敏,小聪,小丽编写的试题分别是下面的(1)(2)(3).
(1)一个不透明的盒子里装有4个红球,2个白球,除颜色外其它都相同,搅均后,从中随意摸出一个球,摸出红球的可能性是多少?解:P(摸出一个红球)=![]() .
.
(2)口袋里装有如图所示的1角硬币2枚、5角硬币2枚、1 元硬币1枚.搅均后,从中随意摸出一枚硬币,摸出1角硬币的可能性是多少?解:P(摸出1角的硬币)=![]() .
.
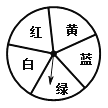
(3)如图,是一个转盘,盘面上有5个全等的扇形区域,每个区域显示有不同的颜色,轻轻转动转盘,当转盘停止后,指针对准红色区域的可能性是多少?解:P(指针对准红色区域)=![]() .
.
问题:根据以上材料回答问题:小敏,小聪,小丽三人中,谁编写的试题及解答是正确的,并简要说明其他两人所编试题或解答的不足之处.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,扇形AOD中,∠AOD=90°,OA=6,点P为![]() 上任意一点(不与点A和D重合),
上任意一点(不与点A和D重合),
PQ⊥OD于点Q,点I为△OPQ的内心,过O、I和D三点的圆的半径为r,则当点P在![]() 上运动时,求r的值.
上运动时,求r的值.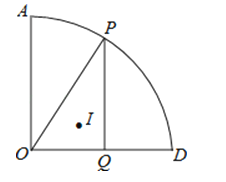
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一项工程,甲乙两人合作需要8天完成任务,若甲单独做需要12天完成任务.
(1)若甲乙两人一起做6天,剩下的由甲单独做,还需要几天完成?
(2)若甲乙两人一起做4天,剩下的由乙单独做,还需要几天完成?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的内切圆,点D、E分别为边AC、BC上的点,且DE为⊙O的切线,若△ABC的周长为25,BC的长是9,则△ADE的周长是( )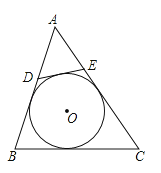
A.7
B.8
C.9
D.16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“微薄问政”当属时下最时髦的词汇之一,今年3月全国人大和政协年度会议期间,不少代表和委员通过微薄与民众进行沟通.3月25日到4月5日,环球舆情调查中心以网络在线调查和电话调查两种方式在北京市就使用微薄动因、关注内容以及“微薄问政”的态度等问题进行了调查, 以下是“微薄问政”的态度的统计图表.
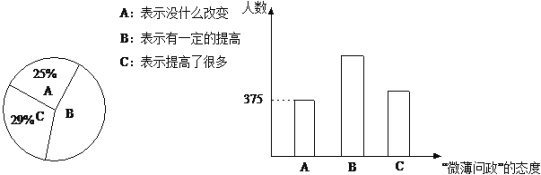
(1)求认为微薄对政治关注的程度有一定提高的人数的百分比;
(2)求在此调查中认为微薄对政治关注的程度提高了很多的人数;
(3)在北京市2500万人口中请你估计一下认为微薄对政治的关注程度没有什么改变的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com