
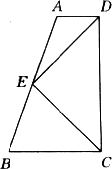
已知如图所示,在梯形ABCD中,AD∥BC,E是AB的中点,DE⊥CE.求证AD+BC=CD.
|
证明:如图所示,延长DE交CB的延长线于点F,
∵AD∥CF, ∴∠F=∠1,∠A=∠2. ∵E为AB中点, 又∵AE=BE, 在△ADE和△BFE中, ∠1=∠F(已证), AE=BE(已证), ∠AED=∠BEF(对顶角相等), ∴△ADE≌△BFE(A.A.S.). ∴EF=ED,AD=BF(全等三角形的对应边相等). ∵CE⊥DE,∴CE⊥DF, ∴DC=CF=BC+BF=BC+AD. 即AD+BC=DC 分析:由E是AB的中点,可以运用旋转变换将△AED绕着E点旋转到△BEF的位置,这样就构成了三线合一的基本图形. |
|
本题属于线段的和差问题,主要思维方法是作出辅助线,使得线段AD和BC转化为一条线段,然后根据三角形全等知识证明. |


 优等生题库系列答案
优等生题库系列答案科目:初中数学 来源: 题型:
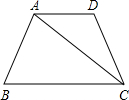 已知如图所示,在梯形ABCD中,AD∥BC,AB=AD=DC=8,∠B=60°,连接AC.
已知如图所示,在梯形ABCD中,AD∥BC,AB=AD=DC=8,∠B=60°,连接AC.查看答案和解析>>
科目:初中数学 来源: 题型:
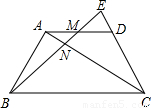
 D的延长线于E.
D的延长线于E.| EM |
| EB |
| AM |
| BC |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
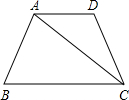 已知如图所示,在梯形ABCD中,AD∥BC,AB=AD=DC=8,∠B=60°,连接AC.
已知如图所示,在梯形ABCD中,AD∥BC,AB=AD=DC=8,∠B=60°,连接AC.查看答案和解析>>
科目:初中数学 来源:巴中 题型:解答题
查看答案和解析>>
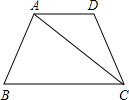
科目:初中数学 来源:2011年四川省巴中市中考数学试卷(解析版) 题型:解答题
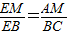 ;
;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com